在介绍堆排序前,我们需要了解一下一种数据结构 —— 顶堆。
什么是顶堆?
它是一颗完全二叉树,顶堆有大顶堆和小顶堆两种。所谓大顶堆就是在这颗完全二叉树中,任何一颗子树都满足:父结点的值 > 孩子结点的值;小顶堆则相反。
如图:
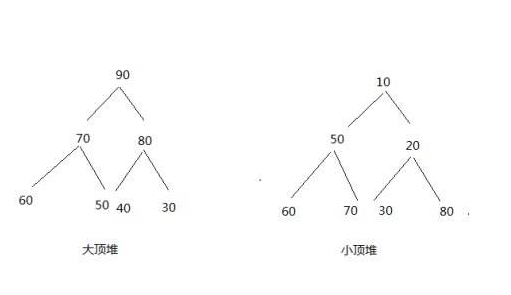
什么是堆排序(heapsort)?
利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。
现在给我们一个无序数组,我们将其从小到大排序,使用堆排序的实现步骤和思想如下:
- 1.让这个数组变成一个大根堆
- 2.将最后一个位置和堆顶位置作交换
- 3.将堆的大小进行 -1 操作
- 4.将当前的堆变成一个大顶堆
- 5.回到2
看起来似乎很抽象,那我们现在用一个例子进行讲解:假设一个整型数组arr = {2, 1, 3, 6, 0, 5}
1.将一个无序数组变成一个大顶堆存储
如果使用完全二叉树进行存储数组,任意下标为index的结点的父结点的下标应该是(index-1)/2,其孩子结点的下标应分别为:(index * 2 + 1) 和 (index * 2 + 2) 。我们使用该结论创建一个大顶堆:
首先我们假设0位置上的数已经排好,将其放在这棵二叉树的根位置,创建一个int类型变量 i 记录当前指向的数组的下标,初始化值为1。
设置一个index初始化值 = i,将index和(index-1)/2位置的数进行比较,也就是和它的父结点进行比较,如果比父结点小就不变,并进行 i++,index = i;如果比父结点大就和父结点交换并且给index赋值为(index-1)/2,即指向原来位置的父结点,再将该值与当前结点的父结点进行比较…直到该结点值是小于该结点父结点的值或到根结点时停止。
以arr数组进行举例:
0位置上的数是2,先认为它是已经排好的,i 和 index此时都为1,(index - 1)/2为0,所以将1和2进行比较,1 < 2 所以1位置上的数不变,执行 i++, index = i;
此时i 和 index值都为2,(index - 1)/2为0,所以讲3 和 2进行比较,3 > 2所以将3和2进行交换,原数组就变为:{3, 1, 2, 6, 0, 5},index = (index - 1)/2 = 0,当前结点是根节点,不再进行比较了,执行 i++, index = i;
此时i 和 index值都为3,(index - 1)/2为 1,所以将 6 和 1 进行比较,6 > 1所以将6和2进行交换,原数组就变为:{3, 6, 2, 1, 0, 5},index = (index - 1)/2 = 1,不是根节点,于是再将6 和 3进行比较,6 > 3,所以再交换6 和 3,原数组变为:{6, 3, 2, 1, 0, 5},index = (index - 1)/2 = 0,当前结点是根节点,不再进行比较了,执行 i++, index = i;
…….
以此类推最后得到的数组:{6, 3, 5, 1, 0, 2}
最后得到的大顶堆:
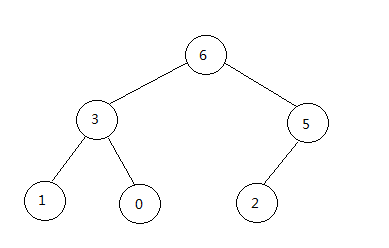
代码实现:
|
1
2
3
4
5
6
7
|
// 插入数使其形成大顶堆public static void heapinsert(int[] arr, int index) { while(arr[index] > arr[(index - 1)/2]) { swap(arr, index, (index - 1)/2); index = (index - 1)/2; }} |
2.将形成的大顶堆最后一个元素和根进行交换
在该例子中应该是将2和6进行交换,得到:
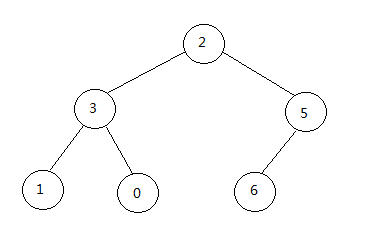
得到的数组:{2, 3, 5, 1, 0, 6}
那我们为什么要进行交换呢?
这时候的数组最后一个值就是最大的了,也就是最后一个位置上的数已经排好了,接下来我们就要将除了最后位置的结点之外剩下的完全二叉树进行排序了,即:
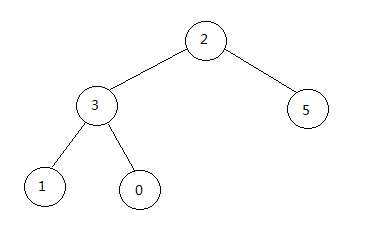
要进行排序的部分:{2, 3, 5, 1, 0}
3.将除了最后一个结点剩下的完全二叉树转化成一个新的大顶堆
传入当前数组,并标记当前位置index,初始化值为0,先判断当前的index位置的结点是否是叶子结点,如果是叶子结点就不需要再比较了,直接返回;如果不是叶子结点,则将index位置的值和它孩子结点的值进行比较,如果index位置上的值最大则不交换并且直接返回,否则选取最大的值与index位置上的值进行交换;交换后index为当前位置,再与当前位置的孩子结点进行比较。。。以此类推直到当前结点是一个叶子结点或不需要再交换时停止。
该例子中:index位置上的值是2,该位置的孩子结点分别为3 和 5,将2和5进行交换之后,index = index * 2 + 2 = 2,此时index位置结点是一个叶子结点,不再进行交换,此时构成了一个新的大顶堆。如图:
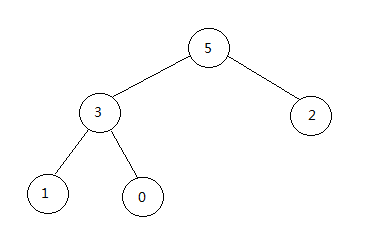
得到的数组:{5, 3, 2, 1, 0, 6}
然后就回到了步骤2,直到数组中未排序的部分只有一个数时不再进行排序。
完整代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
/** * @author lzd 2018/03/01 */public class heapsort { public static void heapsort(int[] arr) { if(arr == null || arr.length < 2) return; // 构建大顶堆 for(int i = 0;i < arr.length;i++) { heapinsert(arr, i); } int heapsize = arr.length; swap(arr, 0, --heapsize); while(heapsize > 0) { heapify(arr, 0, heapsize); swap(arr, 0, --heapsize); } } // 插入数使其形成大顶堆 public static void heapinsert(int[] arr, int index) { while(arr[index] > arr[(index - 1)/2]) { swap(arr, index, (index - 1)/2); index = (index - 1)/2; } } // 将堆化为大顶堆 public static void heapify(int[] arr, int index, int heapsize) { // 先判断当前的index位置的结点是否是叶子结点 int left = index * 2 + 1; while(left < heapsize) { // 不是叶子结点则选出index位置结点的孩子结点中较大的赋给largest int largest = left+1 < heapsize && arr[left + 1] > arr[left] ? left + 1: left; largest = arr[largest] > arr[index] ? largest : index; if(largest == index) { break; } swap(arr, largest, index); index = largest; left = index * 2 + 1; } } public static void swap(int[] arr, int i, int j) { int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp; } // for test 打印数组 public static void printarray(int[] arr) { for(int i = 0;i < arr.length;i++) { system.out.print(arr[i] + " "); } system.out.println(); } // for test public static void main(string[] args) { int[] arr = {2, 1, 3, 6, 0, 5}; heapsort(arr); printarray(arr); }} |
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,谢谢大家对服务器之家的支持。如果你想了解更多相关内容请查看下面相关链接
原文链接:https://blog.csdn.net/sdr_zd/article/details/79705766
















