二叉树在计算机中的存储方式往往线性结构,线性存储分为顺序存储和链式存储,将二叉树按层序编号。
顺序结构:按编号的顺序进行存储,对于完全二叉树而言,顺序存储可以反映二叉树的逻辑,但是对于大多数的二叉树则无法反映其逻辑关系,不过可以用 ^ 来代替不存在的结点,但是如果这个树是一个右斜树,就非常浪费存储空间。所以二叉树的存储形式一般为链式存储结构。
链式存储:每一个结点都分有一个数据域(data)和两个指针域(lchild和rchild),指针域分别指向左孩子和右孩子,若为空则为null。遍历方式有四种:前序遍历、中序遍历、后序遍历及层序遍历,前三种遍历方式采用递归的思想进行遍历。
为方便理解,画一个树并结合代码
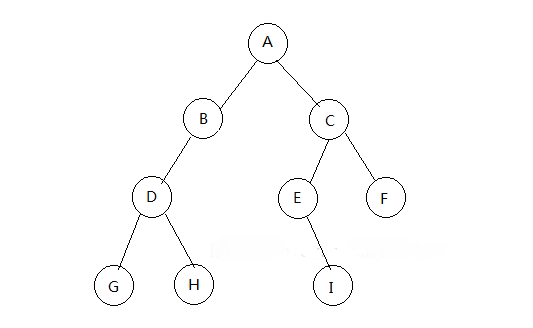
前序遍历:若二叉树为空则返回null,否则先访问根节点然后遍历左子树,再遍历右子树,如图:abdghceif
代码如下:
|
1
2
3
4
5
6
7
|
void preordertraverse(bitree t) { if(t == null) /*为空返回*/ return; printf("%c",t->data); /*输出该结点的信息*/ preordertraverse(t->lchild); /*遍历左子树*/ preordertraverse(t->rchild); /*遍历右子树*/} |
中序遍历:若二叉树为空则返回null,否则从根节点出发访问左子树,然后访问根结点,最后访问右子树,如图:gdhbaeicf
代码如下:
|
1
2
3
4
5
6
7
|
void inordertraverse(bitree t) { if(t == null) /*为空返回*/ return; inordertraverse(t->lchild); /*遍历左子树*/ printf("%c",t->data); /*输出该结点的信息*/ inordertraverse(t->rchild); /*遍历右子树*/} |
后序遍历:若二叉树为空则返回null,否则以先叶子后结点的方式进行访问最后到根结点遍历结束,如图:ghdbiefca
代码如下:
|
1
2
3
4
5
6
7
|
void postordertraverse(bitree t) { if(t == null) /*为空返回*/ return; postordertraverse(t->lchild); /*遍历左子树*/ postordertraverse(t->rchild); /*遍历右子树*/ printf("%c",t->data); /*输出该结点的信息*/} |
层序遍历:若二叉树为空则返回null,否则从第一层开始进行访问,如图:abcdefghi,按编号进行输出或操作即可
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,谢谢大家对服务器之家的支持。如果你想了解更多相关内容请查看下面相关链接
原文链接:https://blog.csdn.net/sdr_zd/article/details/52214723















