确定一个子串(模式串)在主串中第一次出现的位置。
BF算法(Brute-Force算法)
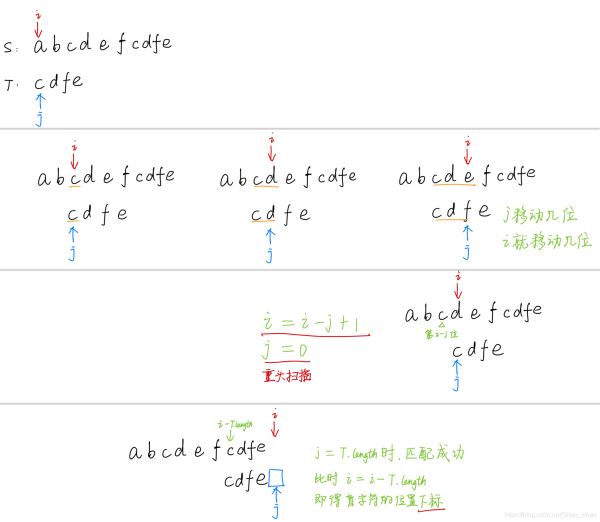
BF算法即朴素的简单匹配法,采用的是穷举的思路。从主串的每一个字符开始依次与模式串的字符进行比较。

int index_BF(SeqString S, SeqString T, int begin)//从S的第begin位(下标)开始进行匹配判断
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (S.ch[i] == T.ch[j])
{
i ++;
j ++;//比较下一个字符
}
else
{
i = i - j + 1;
j = 0;//模式串回溯到起点
}
}
if (j == T.length) return i - T.length; //匹配成功,则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int index_BF(char S[], char T[], int beg)
{
int i = beg, j = 0;
while (i < strlen(S) && j < strlen(T))
{
if (S[i] == T[j])
{
i ++;
j ++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (i == strlen(S)) return i - strlen(T);
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
printf("%d", index_BF(str1, str2, 0));
return 0;
}
KMP算法(快速的)
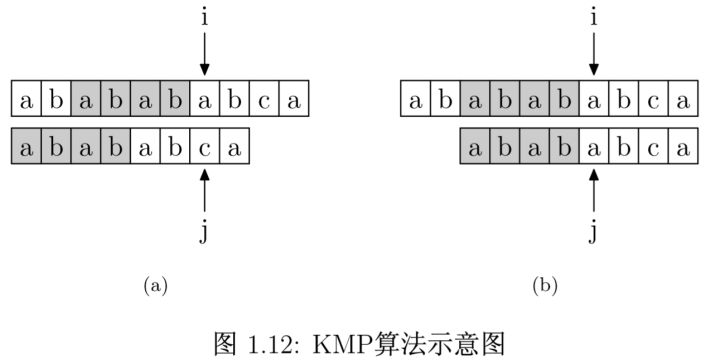
基本思想为:主串的指针 i i i不必回溯,利用已经得到前面“部分匹配”的结果,将模式串向右滑动若干个字符,继续与主串中的当前字符进行比较,减少了一些不必要的比较。
时间复杂度为 O ( n + m )
KMP算法的核心,是一个被称为部分匹配表(Partial Match Table)的数组。
首先要明白什么是字符串的前缀和后缀。
如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”,”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。
同样可以定义后缀A=SB,其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。
要注意的是,字符串本身并不是自己的前缀或后缀。
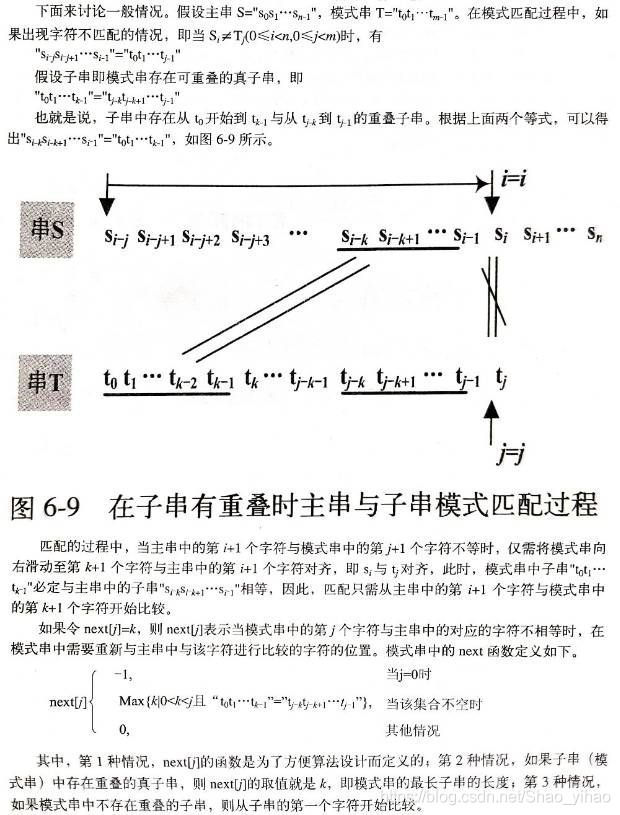
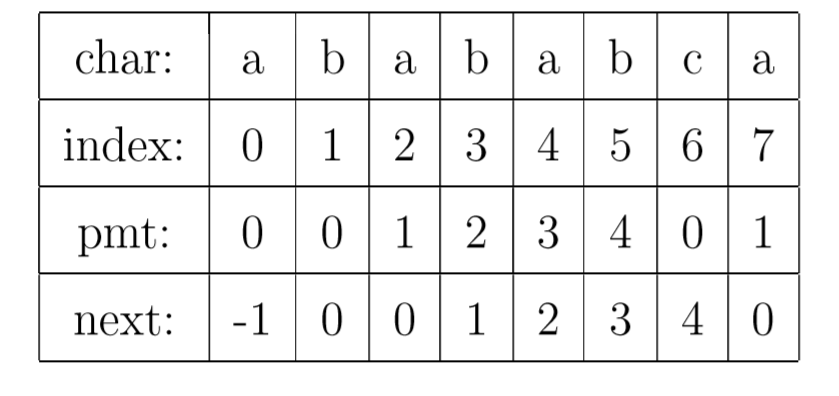
PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
比如,对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3,即该字符串在PMT表中的值为3。性质为:该字符串前3个字符与后三个字符相同。
如果模式串有 j个字符,则PMT表中就有 j 个数值。其中第一个数值总为0。

int index_KMP(SeqString S, SeqString T, int begin)//从S的第begin位(下标)开始进行匹配判断
{
int i = begin, j = 0;
while (i < S.length && j < T.length)
{
if (j == -1 || S.ch[i] == T.ch[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == T.length) return i - T.length; //匹配成功,则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
那么该如何求出next数组呢?

其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前i位置的next值。如下图所示。
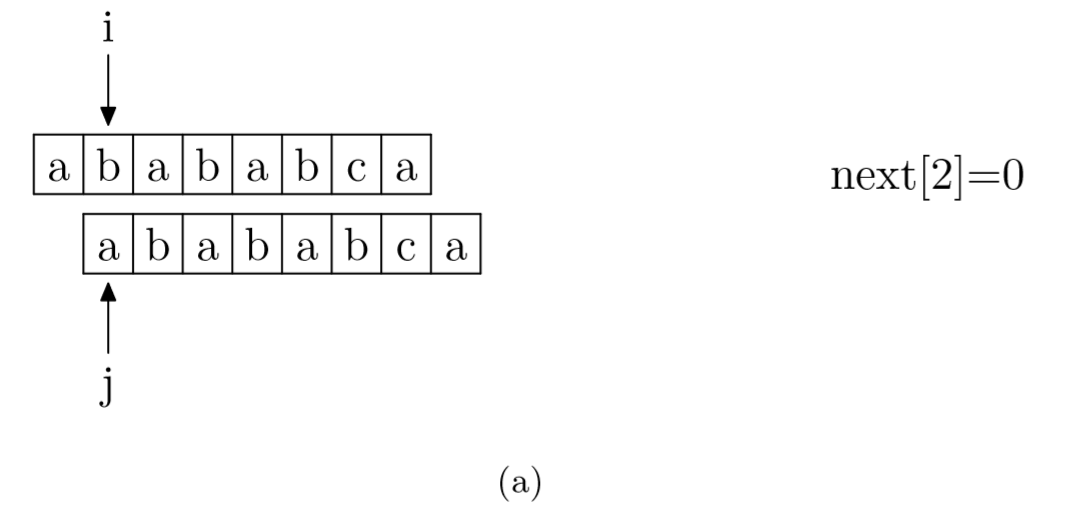
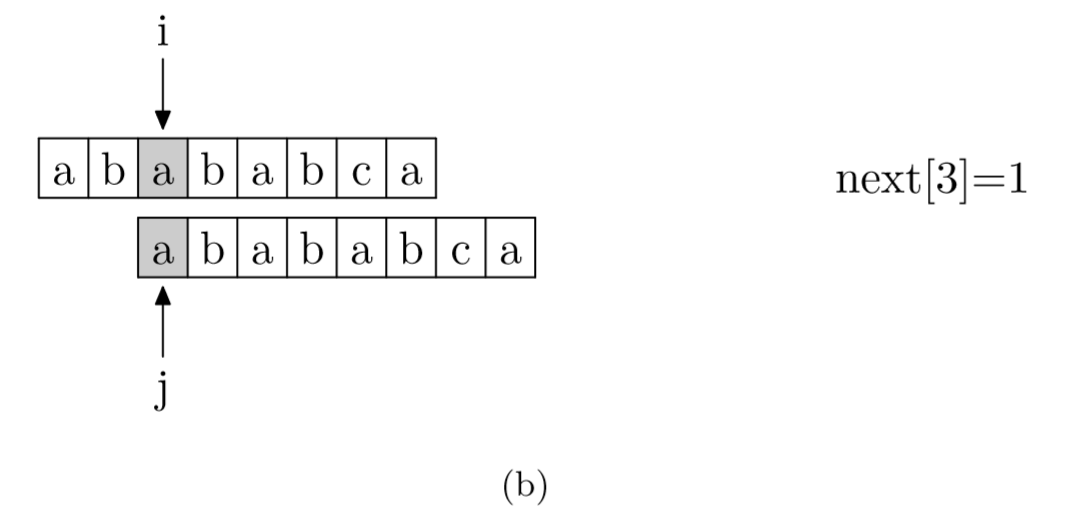
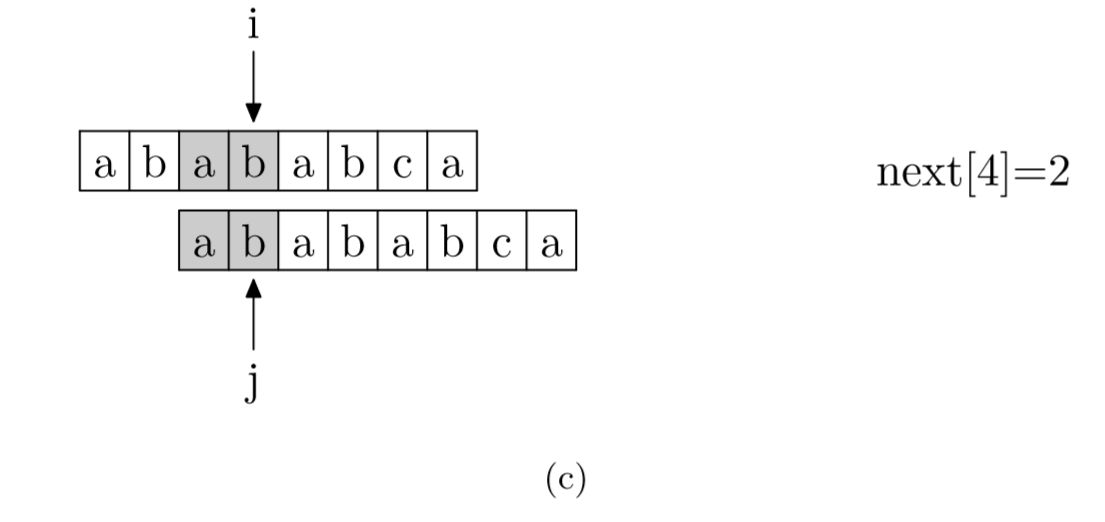
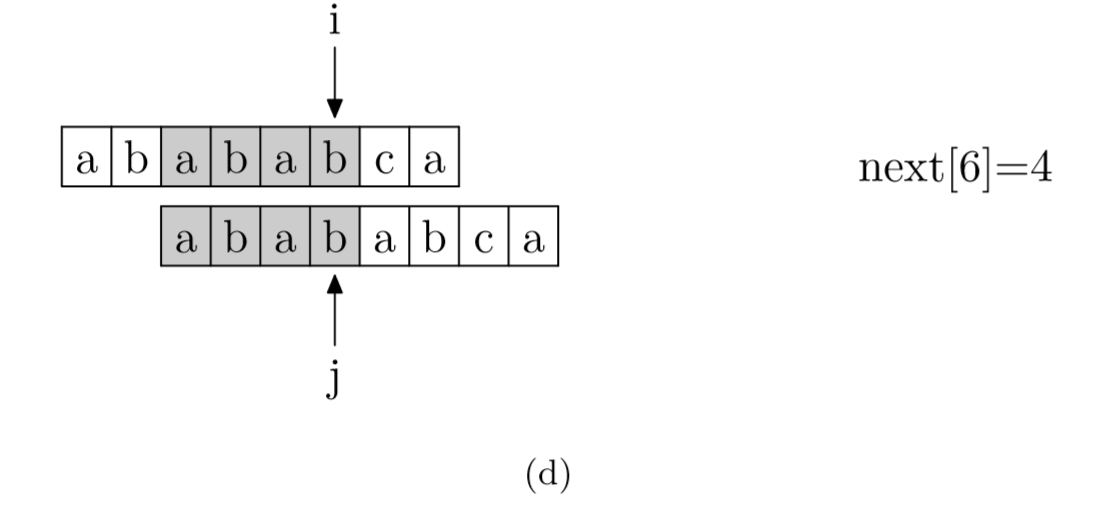
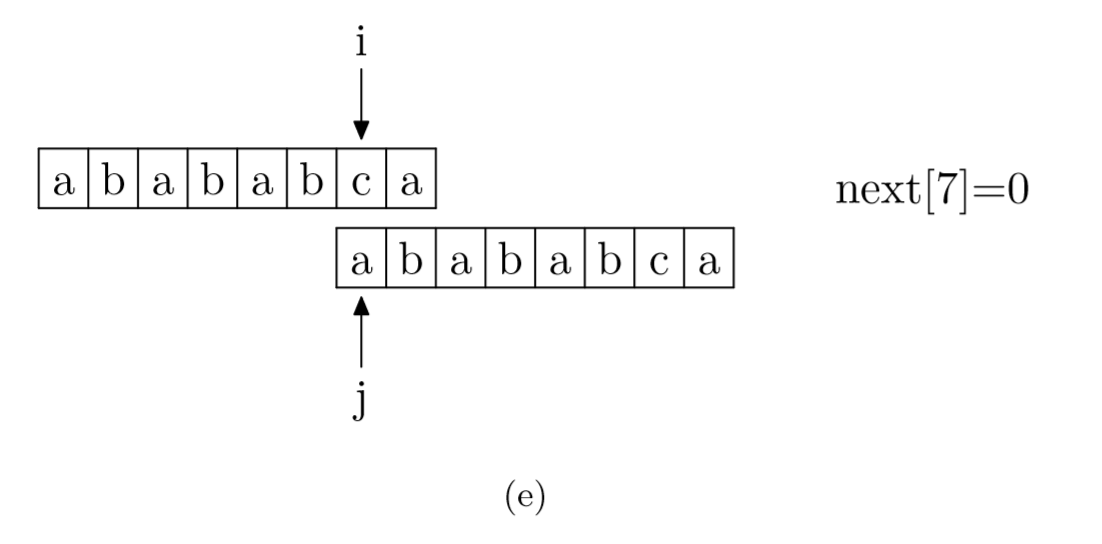
void GetNext(SeqString T, int next[])
{
next[0] = -1;
int j = 0, k = -1;//起始时k落后j一位
while (j < T.length)//j遍历一遍模式串,对于每个字符得到该位置的next数组的值
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
next[j] = k + 1;//将j视为指向一个子串(后缀)结束后的下一个字符,k指向一个子串(前缀)的最后一个字符,则这两个子串的重叠部分的长度(k下标从0开始)即PMT[j-1]的值
k ++;
/*也可以简便地写为(易记):
j ++;
k ++;
next[j] = k;
最简单的形式为:
next[++ j] = ++ k;
*/
}
else k = next[k];//k回溯,即将第二个子串(右滑)(减小匹配的前缀长度)
}
}
即:
#include <stdio.h>
#include <string.h>
int next[10];//全局数组
void GetNext(char T[])
{
int j = 0, k = -1;
next[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
next[j] = k + 1;
k ++;
}
else k = next[k];
}
}
int index_KMP(char S[], char T[], int begin)//从S的第begin位(下标)开始进行匹配判断
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = next[j];//即PMT[j-1]
}
if (j == strlen(T)) return i - strlen(T); //匹配成功,则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "cde";
GetNext(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
求next数组的方法也可进行优化:
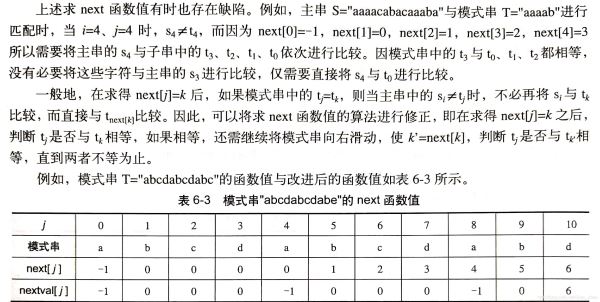
void GetNextVal(SeqString T, int nextval[])
{
nextval[0] = -1;
int j = 0, k = -1;
while (j < T.length)
{
if (k == -1 || T.ch[j] == T.ch[k])
{
j ++;
k ++;
if (T.ch[j] != T.ch[k])
nextval[j] = k;
else
nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
即:
int nextval[10];//全局数组
void GetNextVal(char T[])
{
int j = 0, k = -1;
nextval[0] = -1;
while (j < strlen(T))
{
if (k == -1 || T[j] == T[k])
{
j ++;
k ++;
if (T[j] != T[k]) nextval[j] = k;
else nextval[j] = nextval[k];
}
else k = nextval[k];
}
}
int index_KMP(char S[], char T[], int begin)//从S的第begin位(下标)开始进行匹配判断
{
int i = begin, j = 0;
while (i < strlen(S) && strlen(T))
{
if (j == -1 || S[i] == T[j])
{
i ++;
j ++;
}
else j = nextval[j];
}
if (j == strlen(T)) return i - strlen(T); //匹配成功,则返回该模式串在主串中第一次出现的位置下标
else return -1;
}
int main()
{
char str1[10] = "abcde";
char str2[10] = "bcde";
GetNextVal(str2);
printf("%d", index_KMP(str1, str2, 0));
return 0;
}
KMP―yxc模板
字符串从数组下标1开始存
#include <iostream>
using namespace std;
const int M = 1000010, N = 100010;
char S[M], p[N];
int ne[N]; //全局变量数组,初始化全为0
int main()
{
int m, n;
cin >> m;
for (int i = 1; i <= m; i ++) cin >> S[i];
cin >> n;
for (int i = 1; i <= n; i ++) cin >> p[i];//主串与模式串均由数组下标1开始存储
// 也可以简写为 cin >> m >> S + 1 >> n >> p + 1;
for (int i = 2, j = 0; i <= n; i ++)//求模式串各字符处的next值,即求串p[1~i]的前后缀最大交集的长度
{ //由于字符串由下标1开始存储,next[i]+1也是模式串下次比较的起始下标
while (j && p[i] != p[j + 1]) j = ne[j];//记录的最大交集的长度减小,直到为0,表示p[1~i]前后缀无交集
if (p[i] == p[j + 1]) j ++;//该位匹配成功
ne[i] = j;//j即该位的ne值
}
for (int i = 1, j = 0; i <= m; i ++)//遍历一遍主串
{
while (j && S[i] != p[j + 1]) j = ne[j];//不匹配且并非无路可退,则j后滑。j==0意味着当前i所指的字符与模式串的第一个字符都不一样,只能等该轮循环结束i++,之后再比较
if (S[i] == p[j + 1]) j ++;//该位匹配成功
if (j == n)//主串与模式串匹配成功
{
cout << i - n << ' ';//匹配时,输出 模式串首元素在主串中的下标
j = ne[j];//j后滑,准备继续寻找下一个匹配处
}
}
return 0;
}
字符串从数组下标为开始存
const int N = 1000010;
char s[N], p[N];
int ne[N];
int main()
{
int n, m;
cin >> m >> p >> n >> s;
ne[0] = -1;//ne[0]初始化为-1
for (int i = 1, j = -1; i < m; i ++ )//从模式串的第2位2开始求next值
{
while (j != -1 && p[j + 1] != p[i]) j = ne[j];
if (p[j + 1] == p[i]) j ++ ;
ne[i] = j;
}
for (int i = 0, j = -1; i < n; i ++ )//遍历一遍主串
{
while (j != -1 && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m - 1)//扫描到模式串结尾,说明匹配完成
{
cout << i - j << ' ';
j = ne[j];
}
}
return 0;
}
总结
本篇文章就到这里了,希望能够给你带来帮助,也希望您能够多多关注服务器之家的更多内容!
原文链接:https://blog.csdn.net/Shao_yihao/article/details/120189585














