并查集(Union-Find Set):
一种用于管理分组的数据结构。它具备两个操作:(1)查询元素a和元素b是否为同一组 (2) 将元素a和b合并为同一组。
注意:并查集不能将在同一组的元素拆分为两组。
并查集的实现:
用树来实现。
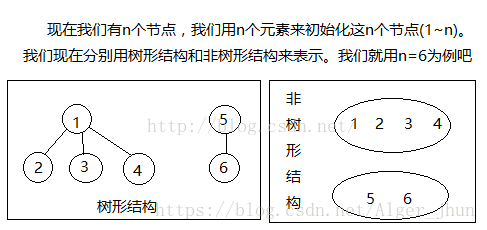
使用树形结构来表示以后,每一组都对应一棵树,然而我们就可以将这个问题转化为树的问题了,我们看两个元素是否为一组我们只要看这两个元素的根是否一致。显然,使用树形结构将问题简单化了。合并时是我们只需要将一组的根与另一组的根相连即可。
并查集的核心在于,一棵树的所有节点根节点都为一个节点。使用Find函数查询时,也是查询到这个节点的根节点。
一行并查集:
|
1
2
3
4
|
int find(int x){ return p[x]==x? x:find(p[x]); //x的父节点保存在p[x]中,如果没有父节点则p[x]=x。} |
实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
int node[i]; //每个节点 //初始化n个节点 void Init(int n){ for(int i = 0; i < n; i++){ node[i] = i; } } //查找当前元素所在树的根节点(代表元素) int find(int x){ if(x == node[x]) return x; return find(node[x]); } //合并元素x, y所处的集合 void Unite(int x, int y){ //查找到x,y的根节点 x = find(x); y = find(y); if(x == y) return ; //将x的根节点与y的根节点相连 node[x] = y; } //判断x,y是属于同一个集合 bool same(int x, int y){ return find(x) == find(y) |
并查集的路径压缩:
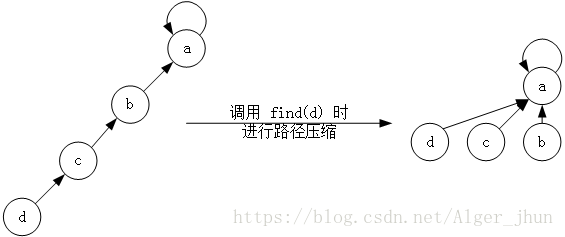
在特殊情况下,这棵树是一条长长的树链,设链的最后一个结点为x,则每次执行find(x)都会遍历整条链。效率十分的地下。 改进方法很简单,只要把遍历过的结点都改成根的子结点,后面的查询就会变的快很多。
并查集的复杂度
加入这两个优化之后,并查集的效率就非常高。对n个元素的并查集操作一次的复杂度是: O(α(n))。这里,α(n)是阿克曼(Ackermann)函数的反函数。效率要高于O(log n)。
不过这里O(α(n))是平均复杂度。也就是说,多次操作之后平均复杂度为O(α(n)),换而言之,并不是每一次操作都满足O(α(n))。
路径压缩后的优化代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
int node[i]; //每个节点 int rank[i]; //树的高度 //初始化n个节点 void Init(int n){ for(int i = 0; i < n; i++){ node[i] = i; rank[i] = 0; } } //查找当前元素所在树的根节点(代表元素) int find(int x){ if(x == node[x]) return x; return node[x] = find(node[x]); //在第一次查找时,将节点直连到根节点 } //合并元素x, y所处的集合 void Unite(int x, int y){ //查找到x,y的根节点 x = find(x); y = find(y); if(x == y) return ; //判断两棵树的高度,然后在决定谁为子树 if(rank[x] < rank[y]){ node[x] = y; }else{ node[y] = x; if(rank[x] == rank[y]) rank[x]++: } } //判断x,y是属于同一个集合 bool same(int x, int y){ return find(x) == find(y); } |
实例分析:
题目:部落
在一个社区里,每个人都有自己的小圈子,还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里,于是要请你统计一下,在一个给定社区中,到底有多少个互不相交的部落?并且检查任意两个人是否属于同一个部落。
输入格式:
输入在第一行给出一个正整数N(<= 104),是已知小圈子的个数。随后N行,每行按下列格式给出一个小圈子里的人:
K P[1] P[2] ... P[K]
其中K是小圈子里的人数,P[i](i=1, .., K)是小圈子里每个人的编号。这里所有人的编号从1开始连续编号,最大编号不会超过104。
之后一行给出一个非负整数Q(<= 104),是查询次数。随后Q行,每行给出一对被查询的人的编号。
输出格式:
首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询,如果他们属于同一个部落,则在一行中输出“Y”,否则输出“N”。
输入样例:
4
3 10 1 2
2 3 4
4 1 5 7 8
3 9 6 4
2
10 5
3 7
输出样例:
10 2
Y
N
分析:典型并查集问题。
一个部落对应一个集合。 根节点数量等于部落数量。
并查集把每个部落的人连起来,记录哪些人出现过,枚举标号10000,找出有多少人和部落,查询并查集维护。
源码分析:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
#include <cstdio>#include <iostream>#include <algorithm>#include <cstring>using namespace std;int pre[10005];int f[10005]; void init() { //初始化父集合pre[10005],以及出现的标志数组f[10005] for(int i=0; i<10004; i++) pre[i]=i, f[i]=0;} int find(int x) { //并查集查找根节点的 递归程序 return pre[x]==x? x : pre[x]=find(pre[x]);} int main(){ init(); int n,q,k,a,b; cin>>n; for(int i=0; i<n; i++) { cin>>k>>a; f[a]=1; for(int j=1; j<k; j++) { cin>>b; f[b]=1; int x=find(a); int y=find(b); if(x!=y) pre[x]=y; } } int cnt=0,tot=0; //cnt为所有人数 tot为部落数量 for(int i=0; i<10004; i++) { if(f[i] == 1) { //如果标志为1 则说明出现过,cnt加一 cnt++; if(pre[i]==i) tot++; //如果下标为本身 说明其为根节点 根节点数量为部落的数量 } } cout<<cnt<<" "<<tot<<endl; cin>>q; for(int i=0; i<q; i++) { cin>>a>>b; if(find(a) == find(b)) //若两参数 有同一根节点 说明为一个部落。 cout<<"Y"<<endl; else cout<<"N"<<endl; } return 0;} |
好了,这篇文章就介绍到这了。
原文链接:https://blog.csdn.net/Alger_jhun/article/details/79730169














