二叉树的特点:每个结点的度最大不能超过2,并且左右子树不能颠倒
二叉树的存储结构:下面采用链式存储进行阐述,堆排序算法(快速排序改进)采用的顺序存储结构的二叉树,先看如下结构体的存储方式
顺序存储:
/*二叉树的顺序存储*/
#define MAX_TREE_SIZE 100
typedef TElemType SqBiTree[MAX_TREE_SIZE];

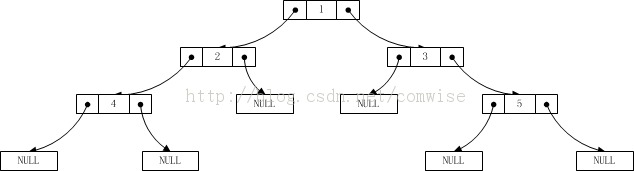
链式存储:
/*二叉树的链式存储*/
typedef struct BiTNode
{
TElemType data;
BiTNode *lchild,*rchild;
}
BiTNode, *BiTree;
这里的TElemType的类型如下,这里我使用了int型的定义:
#define INT_TYPE
#ifdef INT_TYPE
typedef int TElemType;
#elif defined FLOAT_TYPE
typedef float TElemType
#elif defined STRING_TYPE
typedef char *TElemType
#endif
二叉树的创建:这里需要进行递归创建,如下
int CreateBiTree(BiTree &T)
{
int nData;
printf("Please Enter BiTree Node data:\n");
scanf_s("%d", &nData);
if (nData == 0)
{
T = NULL;
return OK;
}
else if (nData > 0 && nData < 100)
{
T = (BiTNode*)malloc(sizeof(BiTNode));
if (!T)
{
return BTOVERFLOW;
}
T->data = nData;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
return OK;
}
#ifdef _DEBUG
printf("Enter data Error!\n");
#endif // _DEBUG
return ERROR;
}
这里我对数据进行了限制,便于进行测试,这里只接受0~100的数据,如果是0表明当前没有孩子的节点(左孩子或者右孩子),如果存在就创建节点,填充数据
遍历二叉树:创建后之后,我必须测试创建的二叉树中的数据是否正确,这里采用的是先根遍历,如下
/*遍历二叉树*/
int PreOrderTraverse(BiTree T, int (*VisitNode)(TElemType))
{
if (T)
{
if (VisitNode(T->data))
{
if (PreOrderTraverse(T->lchild, VisitNode))
{
if (PreOrderTraverse(T->rchild, VisitNode))
{
return OK;
}
}
}
return ERROR;
}
return OK; //如果没有子孩子,这时候应该回溯,要查看右孩子必须为真
}
这里遍历的时候采用了一个函数,注意传递的形参是函数指针,只是进行简单的结点数据的输出,如下:
int VisitNode(TElemType data)
{
#if defined(INT_TYPE) || defined(FLOAT_TYPE)
printf("%d ", data);
#elif defined(STRING_TYPE)
printf("%s ", data);
#endif
return OK;
}
但是在遍历的时候,为什么T为NULL的时候,返回还是OK(1)呢,这里主要是上面的遍历函数的原因,因为这里必须是先遍历左孩子且返回值为真,才能遍历右孩子,所以不能返回ERROR(0),感觉返回值有点怪,修改如下
int PreOrderTraverseEx(BiTree T, int (*VisitNode)(TElemType))
{
if (T)
{
if (VisitNode(T->data))
{
PreOrderTraverse(T->lchild, VisitNode);
PreOrderTraverse(T->rchild, VisitNode);
return OK;
}
}
return ERROR; //如果没有子孩子,这时候应该回溯
}
这样看着就舒服多了,其实可以不使用任何返回值,主要遍历完左右子树不用做其他任何事情,如果还有其他,就不能没有返回值,这里return OK其实要不要也无所谓,因为我根本没有进行判断
测试用例:如下
BiTree T;
if (CreateBiTree(T))
{
PreOrderTraverseEx(T, VisitNode);
printf("\n");
}
这里对测试的数据输入其实有一定的要求,假设根为12 孩子结点为 34 78,这里应该这样输入数据 12 34 0 0 78 0 0,只有这样才能正常退出,如下测试结果:
Please Enter BiTree Node data:
12
Please Enter BiTree Node data:
34
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
78
Please Enter BiTree Node data:
0
Please Enter BiTree Node data:
0
12 34 78
从前面我可以看到这里采用的其实都是递归算法,我们都知道递归最大之弊病就是在每次下潜下一层的时候,一定要保存当前所在层次的数据,具体哪些数据其实是由操作系统OS来进行管理的,但是像每次的形参T一定会入栈,便于在层次退出返回上一层的时候使用,所以这里就可以采用非递归的方式的来进行修改算法:如何做呢?














