本文实例讲述了java矩阵连乘问题(动态规划)算法。分享给大家供大家参考,具体如下:
问题描述:给定n个矩阵:a1,a2,...,an,其中ai与ai+1是可乘的,i=1,2...,n-1。确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵连乘积需要的数乘次数最少。输入数据为矩阵个数和每个矩阵规模,输出结果为计算矩阵连乘积的计算次序和最少数乘次数。
问题解析:由于矩阵乘法满足结合律,故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,也就是说该连乘积已完全加括号,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。
完全加括号的矩阵连乘积可递归地定义为:
(1)单个矩阵是完全加括号的;
(2)矩阵连乘积a是完全加括号的,则a可表示为2个完全加括号的矩阵连乘积b和c的乘积并加括号,即a=(bc)
例如,矩阵连乘积a1a2a3a4有5种不同的完全加括号的方式:(a1(a2(a3a4))),(a1((a2a3)a4)),((a1a2)(a3a4)),((a1(a2a3))a4),(((a1a2)a3)a4)。每一种完全加括号的方式对应于一个矩阵连乘积的计算次序,这决定着作乘积所需要的计算量。
看下面一个例子,计算三个矩阵连乘{a1,a2,a3};维数分别为10*100 , 100*5 , 5*50 按此顺序计算需要的次数((a1*a2)*a3):10x100x5+10x5x50=7500次,按此顺序计算需要的次数(a1*(a2*a3)):10*5*50+10*100*50=75000次
所以问题是:如何确定运算顺序,可以使计算量达到最小化。
算法思路:
例:设要计算矩阵连乘乘积a1a2a3a4a5a6,其中各矩阵的维数分别是:
a1:30*35; a2:35*15; a3:15*5; a4:5*10; a5:10*20; a6:20*25
递推关系:
设计算a[i:j],1≤i≤j≤n,所需要的最少数乘次数m[i,j],则原问题的最优值为m[1,n]。
当i=j时,a[i:j]=ai,因此,m[i][i]=0,i=1,2,…,n
当i<j时,若a[i:j]的最优次序在ak和ak+1之间断开,i<=k<j,则:m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置,所以k还未定。不过k的位置只有j-i个可能。因此,k是这j-i个位置使计算量达到最小的那个位置。
综上,有递推关系如下:
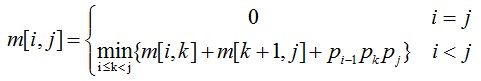
构造最优解:
若将对应m[i][j]的断开位置k记为s[i][j],在计算出最优值m[i][j]后,可递归地由s[i][j]构造出相应的最优解。s[i][j]中的数表明,计算矩阵链a[i:j]的最佳方式应在矩阵ak和ak+1之间断开,即最优的加括号方式应为(a[i:k])(a[k+1:j)。因此,从s[1][n]记录的信息可知计算a[1:n]的最优加括号方式为(a[1:s[1][n]])(a[s[1][n]+1:n]),进一步递推,a[1:s[1][n]]的最优加括号方式为(a[1:s[1][s[1][n]]])(a[s[1][s[1][n]]+1:s[1][s[1][n]]])。同理可以确定a[s[1][n]+1:n]的最优加括号方式在s[s[1][n]+1][n]处断开...照此递推下去,最终可以确定a[1:n]的最优完全加括号方式,及构造出问题的一个最优解。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
package matrix;public class matrix { public static void matrixchain(int[] p,int n, int[][] m, int[][] s) { for (int i = 1; i <= n; i++) { m[i][i] = 0; } for(int r = 2;r <= n; r++ ) { for(int i = 1; i <= n-r+1; i++) { int j = i+r-1; m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j]; s[i][j] = i; for(int k = i+1; k < j; k++) { int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j]; if(t < m[i][j]) { m[i][j] = t; s[i][j] = k; } } } } } public static void traceback(int i, int j, int[][] s) { if(i == j) return; traceback(i,s[i][j],s); traceback(s[i][j] + 1,j,s); system.out.println("multiply a" + i + "," + s[i][j] + "and a" + (s[i][j] + 1) + "," + j); } public static void main(string[] args) { system.out.println("服务器之家测试结果:"); matrix mc = new matrix(); int n = 7; int p[] = { 30, 35, 15, 5, 10, 20, 25 }; int m[][] = new int[n][n]; int s[][] = new int[n][n]; int l = p.length-1; mc.matrixchain(p, l,m, s); for (int i = 1; i < n; i++) { for (int j = 1; j < n; j++) { system.out.print(m[i][j] + "\t"); } system.out.println(); } system.out.println(); for (int i = 1; i < n; i++) { for (int j = 1; j < n; j++) { system.out.print(s[i][j]+" "); } system.out.println(); } mc.traceback( 1, 6, s); }} |
运行结果:
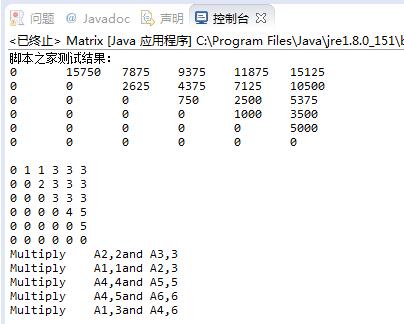
希望本文所述对大家java程序设计有所帮助。
原文链接:http://blog.csdn.net/u014755255/article/details/50571173












