本文研究Keras自带的几个常用的Loss Function。
1. categorical_crossentropy VS. sparse_categorical_crossentropy
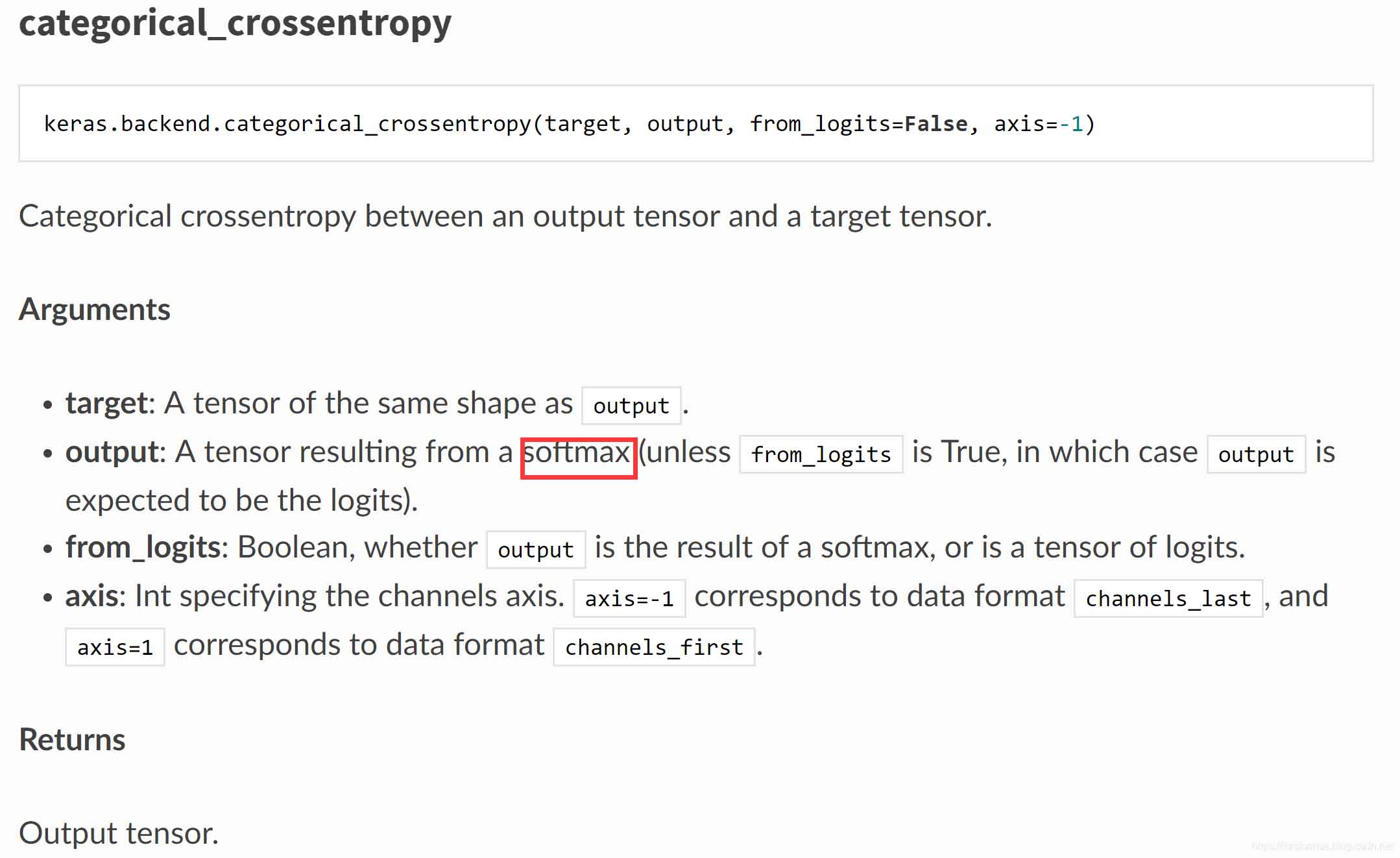

注意到二者的主要差别在于输入是否为integer tensor。在文档中,我们还可以找到关于二者如何选择的描述:

解释一下这里的Integer target 与 Categorical target,实际上Integer target经过独热编码就变成了Categorical target,举例说明:
(类别数5) Integer target: [1,2,4] Categorical target: [[0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 0. 1.]]
在Keras中提供了to_categorical方法来实现二者的转化:
from keras.utils import to_categorical categorical_labels = to_categorical(int_labels, num_classes=None)
注意categorical_crossentropy和sparse_categorical_crossentropy的输入参数output,都是softmax输出的tensor。我们都知道softmax的输出服从多项分布,
因此categorical_crossentropy和sparse_categorical_crossentropy应当应用于多分类问题。
我们再看看这两个的源码,来验证一下:
https://github.com/tensorflow/tensorflow/blob/r1.13/tensorflow/python/keras/backend.py
--------------------------------------------------------------------------------------------------------------------
def categorical_crossentropy(target, output, from_logits=False, axis=-1):
"""Categorical crossentropy between an output tensor and a target tensor.
Arguments:
target: A tensor of the same shape as `output`.
output: A tensor resulting from a softmax
(unless `from_logits` is True, in which
case `output` is expected to be the logits).
from_logits: Boolean, whether `output` is the
result of a softmax, or is a tensor of logits.
axis: Int specifying the channels axis. `axis=-1` corresponds to data
format `channels_last", and `axis=1` corresponds to data format
`channels_first`.
Returns:
Output tensor.
Raises:
ValueError: if `axis` is neither -1 nor one of the axes of `output`.
"""
rank = len(output.shape)
axis = axis % rank
# Note: nn.softmax_cross_entropy_with_logits_v2
# expects logits, Keras expects probabilities.
if not from_logits:
# scale preds so that the class probas of each sample sum to 1
output = output / math_ops.reduce_sum(output, axis, True)
# manual computation of crossentropy
epsilon_ = _to_tensor(epsilon(), output.dtype.base_dtype)
output = clip_ops.clip_by_value(output, epsilon_, 1. - epsilon_)
return -math_ops.reduce_sum(target * math_ops.log(output), axis)
else:
return nn.softmax_cross_entropy_with_logits_v2(labels=target, logits=output)
--------------------------------------------------------------------------------------------------------------------
def sparse_categorical_crossentropy(target, output, from_logits=False, axis=-1):
"""Categorical crossentropy with integer targets.
Arguments:
target: An integer tensor.
output: A tensor resulting from a softmax
(unless `from_logits` is True, in which
case `output` is expected to be the logits).
from_logits: Boolean, whether `output` is the
result of a softmax, or is a tensor of logits.
axis: Int specifying the channels axis. `axis=-1` corresponds to data
format `channels_last", and `axis=1` corresponds to data format
`channels_first`.
Returns:
Output tensor.
Raises:
ValueError: if `axis` is neither -1 nor one of the axes of `output`.
"""
rank = len(output.shape)
axis = axis % rank
if axis != rank - 1:
permutation = list(range(axis)) + list(range(axis + 1, rank)) + [axis]
output = array_ops.transpose(output, perm=permutation)
# Note: nn.sparse_softmax_cross_entropy_with_logits
# expects logits, Keras expects probabilities.
if not from_logits:
epsilon_ = _to_tensor(epsilon(), output.dtype.base_dtype)
output = clip_ops.clip_by_value(output, epsilon_, 1 - epsilon_)
output = math_ops.log(output)
output_shape = output.shape
targets = cast(flatten(target), "int64")
logits = array_ops.reshape(output, [-1, int(output_shape[-1])])
res = nn.sparse_softmax_cross_entropy_with_logits(
labels=targets, logits=logits)
if len(output_shape) >= 3:
# If our output includes timesteps or spatial dimensions we need to reshape
return array_ops.reshape(res, array_ops.shape(output)[:-1])
else:
return res
categorical_crossentropy计算交叉熵时使用的是nn.softmax_cross_entropy_with_logits_v2( labels=targets, logits=logits),而sparse_categorical_crossentropy使用的是nn.sparse_softmax_cross_entropy_with_logits( labels=targets, logits=logits),二者本质并无区别,只是对输入参数logits的要求不同,v2要求的是logits与labels格式相同(即元素也是独热的),而sparse则要求logits的元素是个数值,与上面Integer format和Categorical format的对比含义类似。
综上所述,categorical_crossentropy和sparse_categorical_crossentropy只不过是输入参数target类型上的区别,其loss的计算在本质上没有区别,就是交叉熵;二者是针对多分类(Multi-class)任务的。
2. Binary_crossentropy
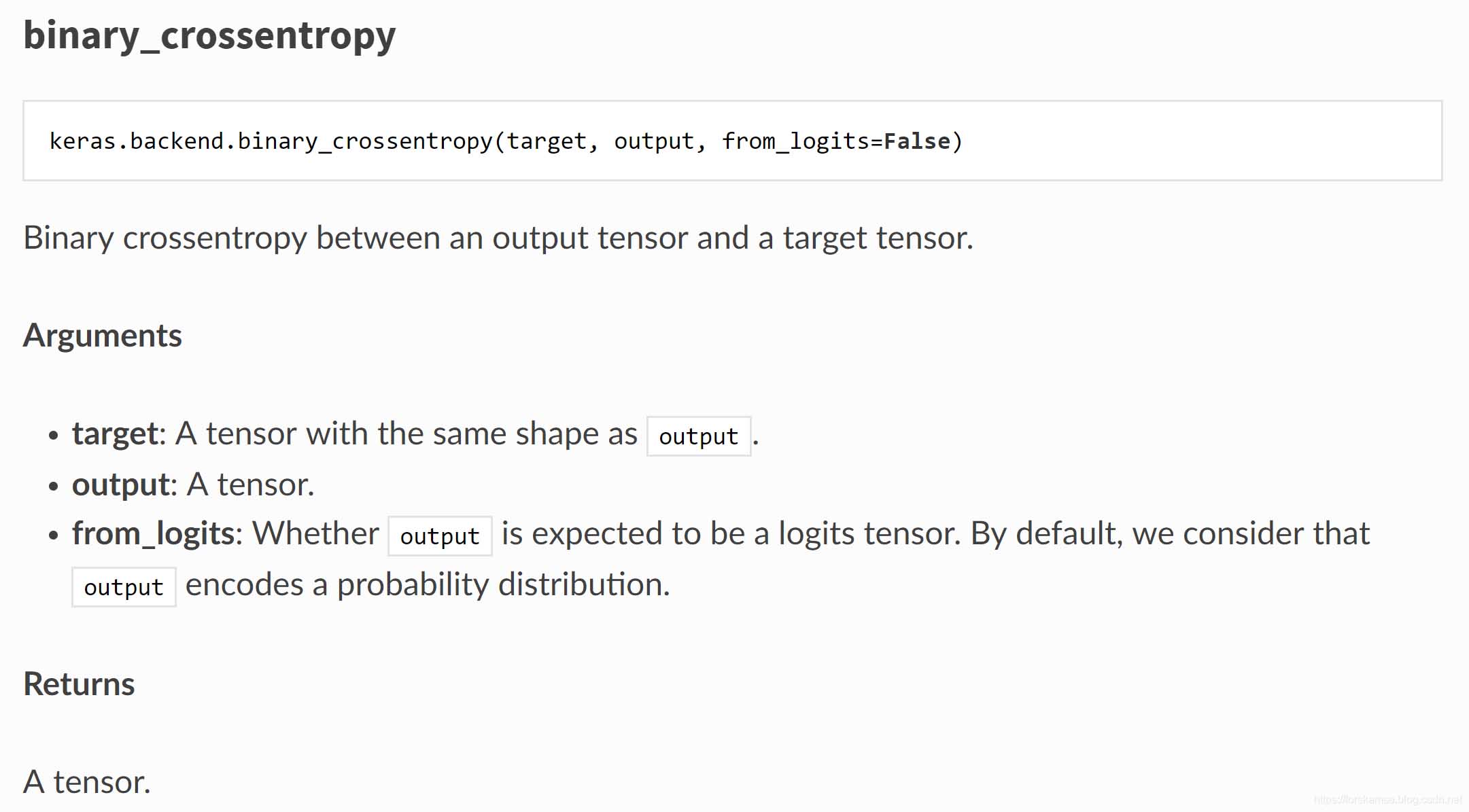
二元交叉熵,从名字中我们可以看出,这个loss function可能是适用于二分类的。文档中并没有详细说明,那么直接看看源码吧:
https://github.com/tensorflow/tensorflow/blob/r1.13/tensorflow/python/keras/backend.py
--------------------------------------------------------------------------------------------------------------------
def binary_crossentropy(target, output, from_logits=False):
"""Binary crossentropy between an output tensor and a target tensor.
Arguments:
target: A tensor with the same shape as `output`.
output: A tensor.
from_logits: Whether `output` is expected to be a logits tensor.
By default, we consider that `output`
encodes a probability distribution.
Returns:
A tensor.
"""
# Note: nn.sigmoid_cross_entropy_with_logits
# expects logits, Keras expects probabilities.
if not from_logits:
# transform back to logits
epsilon_ = _to_tensor(epsilon(), output.dtype.base_dtype)
output = clip_ops.clip_by_value(output, epsilon_, 1 - epsilon_)
output = math_ops.log(output / (1 - output))
return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output)
可以看到源码中计算使用了nn.sigmoid_cross_entropy_with_logits,熟悉tensorflow的应该比较熟悉这个损失函数了,它可以用于简单的二分类,也可以用于多标签任务,而且应用广泛,在样本合理的情况下(如不存在类别不均衡等问题)的情况下,通常可以直接使用。
补充:keras自定义loss function的简单方法
首先看一下Keras中我们常用到的目标函数(如mse,mae等)是如何定义的
from keras import backend as K
def mean_squared_error(y_true, y_pred):
return K.mean(K.square(y_pred - y_true), axis=-1)
def mean_absolute_error(y_true, y_pred):
return K.mean(K.abs(y_pred - y_true), axis=-1)
def mean_absolute_percentage_error(y_true, y_pred):
diff = K.abs((y_true - y_pred) / K.clip(K.abs(y_true), K.epsilon(), np.inf))
return 100. * K.mean(diff, axis=-1)
def categorical_crossentropy(y_true, y_pred):
"""Expects a binary class matrix instead of a vector of scalar classes.
"""
return K.categorical_crossentropy(y_pred, y_true)
def sparse_categorical_crossentropy(y_true, y_pred):
"""expects an array of integer classes.
Note: labels shape must have the same number of dimensions as output shape.
If you get a shape error, add a length-1 dimension to labels.
"""
return K.sparse_categorical_crossentropy(y_pred, y_true)
def binary_crossentropy(y_true, y_pred):
return K.mean(K.binary_crossentropy(y_pred, y_true), axis=-1)
def kullback_leibler_divergence(y_true, y_pred):
y_true = K.clip(y_true, K.epsilon(), 1)
y_pred = K.clip(y_pred, K.epsilon(), 1)
return K.sum(y_true * K.log(y_true / y_pred), axis=-1)
def poisson(y_true, y_pred):
return K.mean(y_pred - y_true * K.log(y_pred + K.epsilon()), axis=-1)
def cosine_proximity(y_true, y_pred):
y_true = K.l2_normalize(y_true, axis=-1)
y_pred = K.l2_normalize(y_pred, axis=-1)
return -K.mean(y_true * y_pred, axis=-1)
所以仿照以上的方法,可以自己定义特定任务的目标函数。比如:定义预测值与真实值的差
from keras import backend as K
def new_loss(y_true,y_pred):
return K.mean((y_pred-y_true),axis = -1)
然后,应用你自己定义的目标函数进行编译
from keras import backend as K
def my_loss(y_true,y_pred):
return K.mean((y_pred-y_true),axis = -1)
model.compile(optimizer=optimizers.RMSprop(lr),loss=my_loss,
metrics=["accuracy"])
以上为个人经验,希望能给大家一个参考,也希望大家多多支持服务器之家。
原文链接:https://forskamse.blog.csdn.net/article/details/89426537










