function recursion(函数递归)
函数递归: 是在 一个 过程 或 函数 在其定义或说明中有 直接 或 间接 调用自身 的一种方法
通常把一个 大型复杂的问题 层层 传化 为一个与 原理相似的 ,规模较小 的问题
递归策略 只需 少量的程序 就可以描述出 解题过程 所需的 多次 重复 计算,大大减少了程序的代码量
递归的中心思想为:
大事化小。
程序一
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include<stdio.h>int main(){ printf("hehe"); main();//陷入死循环,但因为栈溢出,最后会停下来 == stack overflow - 栈溢出 任何一次函数调用,它都会向内存申请空间,分为三部分 栈区,堆区,静态区 栈区 :局部变量,函数的形参堆区: 动态开辟的内存 - malloc(分配内存) and calloc(动态内存分配并初始化零) 静态区: 全局变量,static修饰的变量 return 0;} |
递归的两个必要条件
1,存在限制条件,当满足这个限制条件的时候,递归将不再继续
2.每次递归调用之后越来越接近这个条件
程序一:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#include<stdio.h>一共调用三次 1 2 3void print(int n)// n == 123 void print(int n)n == 12 void print(int n) m == 1 { // { { if (n > 9) // if (n > 9) if (n > 9) { // { { print(n / 10);// 这里再调用 print 函数 print(n / 10); print(n / 10); } // } } printf("%d ",n%10); // 最后打印3 // printf("%d ",n%10); 再打印个2 printf("%d ",n%10); 首先打印 1} // } } int main(){ unsigned int num = 0; scanf("%d",&num);//123 //递归 print(num);//1 2 3 return 0;} |
程序二:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<stdio.h>#include<string.h>写法1(计数器)int my_strlen(char* str)//str指针变量,需要返回整形{ int count = 0; while (*str != '\0') { count++; str ++; } return count;}写法2(递归)int my_strlen(char* str)//str指针变量,需要返回整形{ if (*str != '\0') { return 1 + my_strlen(str + 1); } else return 0;}int main(){ char arr[] = "bit"; //int len = strlen(arr); //printf("%d\n", len); //模拟实现一个strlen函数 int len = my_strlen(arr); printf("len = %d\n",len); return 0;} |
练习
求n的阶乘
迭代与递归
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
#include<stdio.h>1 迭代方式 int facl(int n){ int i = 0; int ret = 1; for (i = 1; i <= n; i++) { ret = ret*i; } return ret;}递归方式int facl(int n){ if (n <= 1) { return 1; } else return n*facl(n - 1); 这里说明一下思维 假设 我们 要求 10 的阶乘 1x1x2x3x4x5x6x7x8x9x10 我们的 n 一开始是 10, 10*facl(n-1) ,其实 facl 函数 就是 把 10 减一,递归就好像是循环,循环的目的,就是 得到 10每次减一的结果,直到它等于1,再让其链接起来, 你可以这么看 10 *(9 * (8 * (7 * ((6 * (5 * (4 *(3 * (2 * (1 * (1)))))))))) 等价于 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 * 1}int main(){ int n = 0; scanf("%d",&n); int ret = facl(n);//循环方式 printf("%d\n",ret); return 0;} |
再来道例题
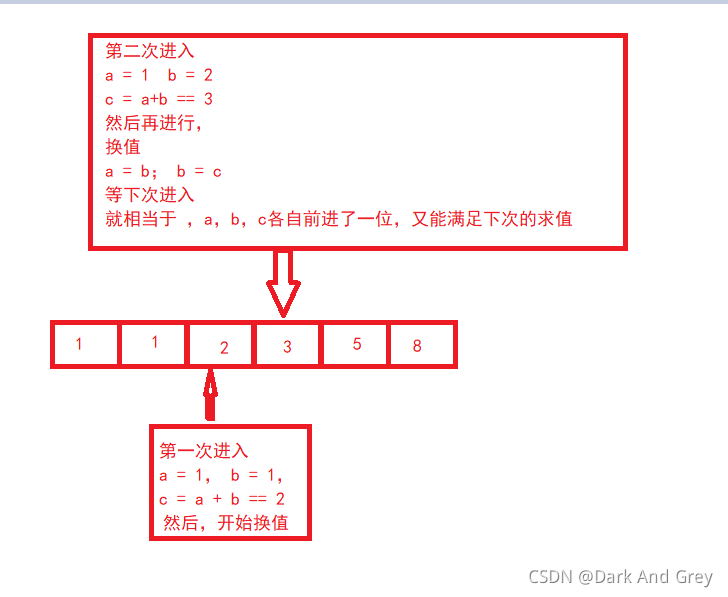
斐波那契函数 1 1 2 3 5 8 13 21
从 第三个数 开始,该数等前面两个数的和。
求第第n个斐波那契函数
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<stdio.h>这题用递归效率很低,很多数会重复计算int fib(int n){ if (n <= 2) return 1; else return fib(n - 1)+fib(n - 2);// 因为 函数 每得到一个数,就需要将得到的数进行分解成 2个 部分}2迭代(循环)方式(简单加法)效率更高int fib(int n){ int a = 1; int b = 1; int c = 1; while (n>2)// { c = a + b; a = b; b = c; n--; } return c;}int main(){ int n = 0; scanf("%d",&n); int ret = fib(n); printf("%d\n",ret); return 0;} |
到此这篇关于C语言 function recursion函数递归详解的文章就介绍到这了,更多相关C语言 函数递归内容请搜索服务器之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持服务器之家!
原文链接:https://blog.csdn.net/DarkAndGrey/article/details/120605939














