理想高通滤波实现 python opencv
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
import numpy as np import cv2 from matplotlib import pyplot as pltplt.rcparams[‘font.sans-serif']=[‘simhei'] plt.rcparams[‘axes.unicode_minus'] = false i = cv2.imread(‘capture3.png') cv2.imshow(‘original',i) (r,g,b) = cv2.split(i) i = cv2.merge([b,g,r]) j = np.double(cv2.cvtcolor(i,cv2.color_rgb2gray)) d1 = 30d2 = 60d3 = 160fuv = np.fft.fftshift(np.fft.fft2(j)) print(‘fuv',fuv) print(i.shape) m,n = i.shape[0],i.shape[1] xo = np.floor(m/2) yo = np.floor(n/2) h1 = np.zeros((m,n)) h2 = np.zeros((m,n)) h3 = np.zeros((m,n)) for i in range(m): for j in range(n): d = np.sqrt((i-xo)**2+(j-yo)**2) if d>=d1: h1[i,j]=1else: h1[i,j]=0if d>=d2: h2[i,j]=1else: h2[i,j]=0if d>=d3: h3[i,j]=1else: h3[i,j]=0guv1 = h1*fuv guv2 = h2*fuv guv3 = h3*fuv g1 = np.fft.ifftshift(guv1) g1 = np.uint8(np.real(np.fft.ifft2(g1))) print(‘g1',g1) g2 = np.fft.ifftshift(guv2) g2 = np.uint8(np.real(np.fft.ifft2(g2))) print(‘g2',g2) g3 = np.fft.ifftshift(guv3) g3 = np.uint8(np.real(np.fft.ifft2(g3))) print(‘g3',g3) plt.subplot(2,2,1),plt.imshow(i),plt.title(‘原图像') plt.subplot(2,2,2),plt.imshow(g1),plt.title(‘d0=30') plt.subplot(2,2,3),plt.imshow(g2),plt.title(‘d0=60') plt.subplot(2,2,4),plt.imshow(g3),plt.title(‘d0=160') plt.show() |
效果:
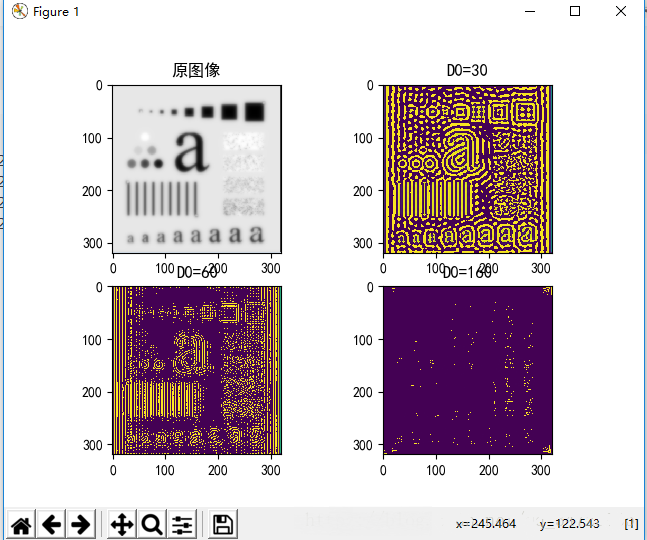
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,谢谢大家对服务器之家的支持。如果你想了解更多相关内容请查看下面相关链接
原文链接:https://blog.csdn.net/qq_34725005/article/details/82695309










