需求说明
在对图像进行处理时,经常会有这类需求:想通过阈值对图像进行二值化分割,以提取自己感兴趣的区域,常见的阈值分割方法有常数分割、最大类间方差法、双峰分割、三角法等等,不同的场景应用不同的阈值方法。
今天要讲的方法,适合当图像的直方图具有明显单峰特征时使用,结合了三角法的原理而设计,相比较OpenCV自带的三角法,好处是可以根据自身需求合理修改函数;如果用OpenCV库的函数,只有一个接口,若不能达到较理想的应用效果,就束手无策了。
下面介绍具体实现流程。
具体流程
1)取图像的灰度图,并遍历统计0-255各个灰度值所出现的次数。
cv::Mat src = imread("test.jpg", 0);
cv::Mat hist = cv::Mat::zeros(1, 256, CV_32FC1);
for (int i = 0; i < src.rows; ++i)
{
for (int j = 0; j < src.cols; ++j)
{
hist.at<float>(0, src.at <uchar>(i, j))++;
}
}
2)去除0和255的直方图数据,这一步就是OpenCV三角法所没有的。很多人可能不理解为什么要这一步,在你对图像进行阈值化时如果提前进行了相关的运算,可能导致结果大于255的数值全部变为255,或者数值低于0的数值全部变为0,这就使得0和255的数值其实涵盖了许多数值,呈累加态,很容易形成双峰,这样就很难找到我们真正想要的峰。例如0和255的数值都是10000左右,0略大一些,而我们的真峰是在250左右的灰度值,数值只有8000多,那么在后续阈值计算时就会因为峰的方向错了而带来毁灭性打击。别觉得我说夸张了,只有自己去碰碰壁才能深刻领悟我说的。
hist.at<float>(0, 255) = 0; hist.at<float>(0, 0) = 0;
3)确认峰值位置,maxidx是峰值对应的灰度值,max是峰值高度,也是灰度值对应数据的个数。
float max = 0;
int maxidx = 0;
for (int i = 0; i < 256; ++i)
{
if (hist.at<float>(0, i) > max)
{
max = hist.at<float>(0, i);
maxidx = i;
}
}
4)判断峰值在左侧还是右侧,true为左侧,false为右侧。
bool lr = maxidx < 127;
5)当在左侧时,连接峰值(maxidx,max)和(255,0)点,用两点建立直线公式,如下图所示公式。 L的表达式可以转换为Ax+By+C=0的形式,A是-max,B是maxidx-255,C是max*255,在结合距离公式可以计算出直方图曲线上每个点到直线的距离,取距离最长的那个点作为阈值。
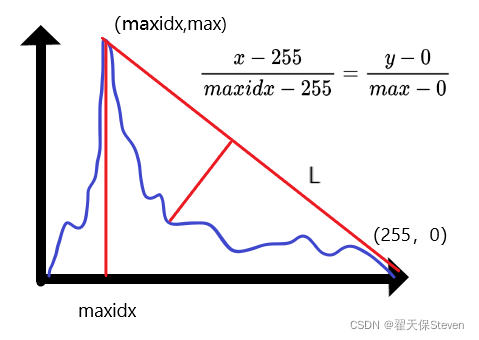
if (lr)
{
float A = float(-max);
float B = float(maxidx - 255);
float C = float(max * 255);
for (int i = maxidx + 1; i < 256; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
6)右侧同理,连接峰值(maxidx,max)和(0,0)点,公式ABC如代码所示。
else {
float A = float(-max);
float B = float(maxidx);
float C = 0.0f;
for (int i = 0; i < maxidx; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
7)二值化,完成。
result.setTo(255, src > maxdidx); idx = maxdidx; return result;
功能函数
// 单峰三角阈值法
cv::Mat Thresh_Unimodal(cv::Mat &src, int& idx)
{
cv::Mat result = cv::Mat::zeros(src.size(), CV_8UC1);
// 统计直方图
cv::Mat hist = cv::Mat::zeros(1, 256, CV_32FC1);
for (int i = 0; i < src.rows; ++i)
{
for (int j = 0; j < src.cols; ++j)
{
hist.at<float>(0, src.at<uchar>(i, j))++;
}
}
hist.at<float>(0, 255) = 0;
hist.at<float>(0, 0) = 0;
// 搜索最大值位置
float max = 0;
int maxidx = 0;
for (int i = 0; i < 256; ++i)
{
if (hist.at<float>(0, i) > max)
{
max = hist.at<float>(0, i);
maxidx = i;
}
}
// 判断最大点在哪一侧,true为左侧,false为右侧
bool lr = maxidx < 127;
float maxd = 0;
int maxdidx = 0;
// 假设在左侧
if (lr)
{
float A = float(-max);
float B = float(maxidx - 255);
float C = float(max * 255);
for (int i = maxidx + 1; i < 256; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
// 假设在右侧
else {
float A = float(-max);
float B = float(maxidx);
float C = 0.0f;
for (int i = 0; i < maxidx; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
// 二值化
result.setTo(255, src > maxdidx);
idx = maxdidx;
return result;
}
C++测试代码
#include <iostream>
#include <time.h>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
cv::Mat DrawHistImg(cv::Mat &hist);
cv::Mat Thresh_Unimodal(cv::Mat &src, int& idx);
int main()
{
cv::Mat src = imread("test.jpg", 0);
// 绘制均衡化后直方图
cv::Mat hrI = DrawHistImg(src);
// 单峰三角阈值法
int thresh;
cv::Mat result = Thresh_Unimodal(src, thresh);
cout << " thresh: " << thresh << endl;
imshow("original", src);
imshow("hist", hrI);
imshow("result", result);
waitKey(0);
return 0;
}
// 绘制简易直方图
cv::Mat DrawHistImg(cv::Mat &src)
{
cv::Mat hist = cv::Mat::zeros(1, 256, CV_32FC1);
for (int i = 0; i < src.rows; ++i)
{
for (int j = 0; j < src.cols; ++j)
{
hist.at<float>(0, src.at <uchar>(i, j))++;
}
}
cv::Mat histImage = cv::Mat::zeros(540, 1020, CV_8UC1);
const int bins = 255;
double maxValue;
cv::Point2i maxLoc;
cv::minMaxLoc(hist, 0, &maxValue, 0, &maxLoc);
int scale = 4;
int histHeight = 540;
for (int i = 0; i < bins; i++)
{
float binValue = (hist.at<float>(i));
int height = cvRound(binValue * histHeight / maxValue);
cv::rectangle(histImage, cv::Point(i * scale, histHeight),
cv::Point((i + 1) * scale - 1, histHeight - height), cv::Scalar(255), -1);
}
return histImage;
}
// 单峰三角阈值法
cv::Mat Thresh_Unimodal(cv::Mat &src, int& idx)
{
cv::Mat result = cv::Mat::zeros(src.size(), CV_8UC1);
// 统计直方图
cv::Mat hist = cv::Mat::zeros(1, 256, CV_32FC1);
for (int i = 0; i < src.rows; ++i)
{
for (int j = 0; j < src.cols; ++j)
{
hist.at<float>(0, src.at<uchar>(i, j))++;
}
}
hist.at<float>(0, 255) = 0;
hist.at<float>(0, 0) = 0;
// 搜索最大值位置
float max = 0;
int maxidx = 0;
for (int i = 0; i < 256; ++i)
{
if (hist.at<float>(0, i) > max)
{
max = hist.at<float>(0, i);
maxidx = i;
}
}
// 判断最大点在哪一侧,true为左侧,false为右侧
bool lr = maxidx < 127;
float maxd = 0;
int maxdidx = 0;
// 假设在左侧
if (lr)
{
float A = float(-max);
float B = float(maxidx - 255);
float C = float(max * 255);
for (int i = maxidx + 1; i < 256; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
// 假设在右侧
else {
float A = float(-max);
float B = float(maxidx);
float C = 0.0f;
for (int i = 0; i < maxidx; ++i)
{
float x0 = float(i);
float y0 = hist.at<float>(0, i);
float d = abs(A * x0 + B * y0 + C) / std::sqrt(A * A + B * B);
if (d > maxd)
{
maxd = d;
maxdidx = i;
}
}
}
// 二值化
result.setTo(255, src > maxdidx);
idx = maxdidx;
return result;
}
测试效果

图1 原图灰度图
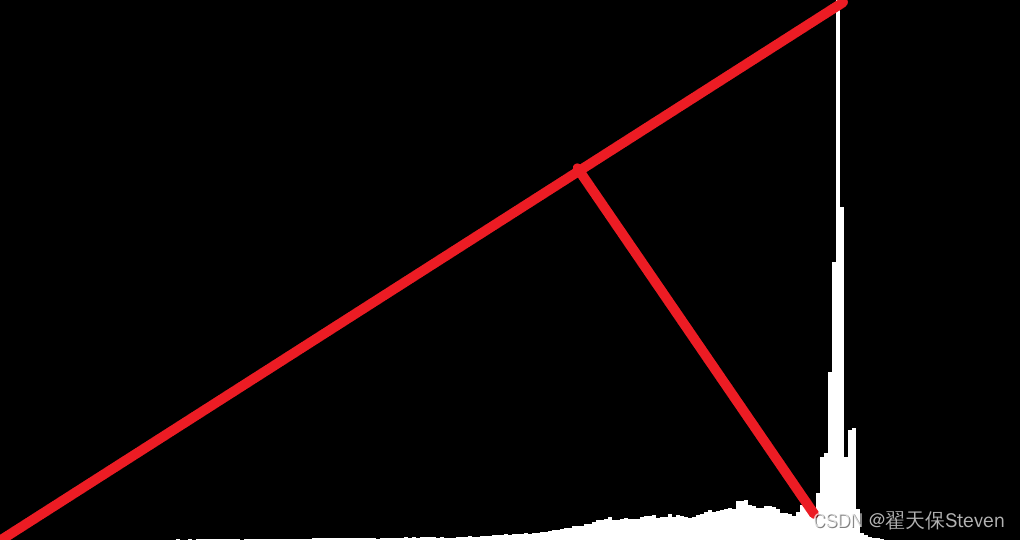
图2 直方图

图3 阈值图
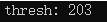
图4 阈值结果
通过imagewatch插件可以观察阈值203是不是在距离最远的位置,答案是肯定的。
如果函数有什么可以改进完善的地方,非常欢迎大家指出,一同进步何乐而不为呢~
以上就是C++ OpenCV单峰三角阈值法Thresh_Unimodal详解的详细内容,更多关于C++ OpenCV单峰三角阈值法的资料请关注服务器之家其它相关文章!
原文链接:https://blog.csdn.net/zhaitianbao/article/details/121790192














