IRIS数据集简介
IRIS数据集中的数据源于1936年费希尔法发表的一篇论文。彼时他收集了三种鸢尾花(分别标记为setosa、versicolor和virginical)的花萼和花瓣数据。包括花萼的长度和宽度,以及花瓣的长度和宽度。我们将根据这四个特征来建立支持向量机模型从而实现对三种鸢尾花的分类判别任务。
有关数据可以从datasets软件包中的iris数据集里获取,下面我们演示性地列出了前5行数据。成功载入数据后,易见其中共包含了150个样本(被标记为setosa、versicolor和virginica的样本各50个),以及四个样本特征,分别是Sepal.Length、Sepal.Width、Petal.Length和Petal.Width。
> iris Sepal.Length Sepal.Width Petal.Length Petal.Width Species 1 5.1 3.5 1.4 0.2 setosa 2 4.9 3.0 1.4 0.2 setosa 3 4.7 3.2 1.3 0.2 setosa 4 4.6 3.1 1.5 0.2 setosa 5 5.0 3.6 1.4 0.2 setosa 6 5.4 3.9 1.7 0.4 setosa 7 4.6 3.4 1.4 0.3 setosa 8 5.0 3.4 1.5 0.2 setosa 9 4.4 2.9 1.4 0.2 setosa 10 4.9 3.1 1.5 0.1 setosa
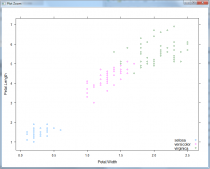
在正式建模之前,我们也可以通过一个图型来初步判定一下数据的分布情况,为此在R中使用如下代码来绘制(仅选择Petal.Length和Petal.Width这两个特征时)数据的划分情况。
library(lattice)
xyplot(Petal.Length ~ Petal.Width, data = iris,
groups = Species,
auto.key = list(corner=c(1, 0)))
上述代码的执行结果如图14-13所示,从中不难发现,标记为setosa的鸢尾花可以很容易地被划分出来。但仅使用Petal.Length和Petal.Width这两个特征时,versicolor和virginica之间尚不是线性可分的。

函数svm()在建立支持向量机分类模型时有两种方式。第一种是根据既定公式建立模型,此时的函数使用格式为:
svm(formula, data= NULL, subset, na.action = na.omit , scale= TRUE)
其中:
- formula表示函数模型的形式
- data表示在模型中包含的有变量的一组可选格式数据
- 参数na.action用于指定当样本数据中存在无效的空数据时系统应该进行怎样的处理。默认值na.omit表示程序会忽略那些数据缺失的样本。另外一个可选的赋值为na.fail,它指示系统在遇到空数据时给出一条错误信息。
- 参数scale为一个逻辑向量指定特征是护具是否需要标准化(默认标准化为均值0,方差1)
- 索引向量subset用于指定那些将来将被用来训练模型的采样数据。
例如,已经知道仅用Petal.Length和Petal.Width这两个特征时标记为setosa和versicolor的鸢尾花是线性可分的,所以我们用下面的代码来构建SVM模型:
data(iris)
attach(iris)
subdata <- iris[iris$Species != 'virginica', ]
subdata$Speices <- factor(subdata$Species)
model1 <- svm(Species ~ Petal.Length + Petal.Width,
data = subdata)
plot(model1, subdata, Petal.Length ~ Petal.Width)
绘制的模型如下:

在使用第一种格式建立模型时,若使用数据中的全部特征变量作为模型特征变量时,可以简要地使用“Species~.”中的“.”代替全部的特征变量。例如下面的代码就利用了全部四种特征来对三种鸢尾花进行分类。
model2 <- svm(Species~., data = iris) summary(model2)
summary函数的结果如下:
> model2 <- svm(Species~., data = iris)
> summary(model2)
Call:
svm(formula = Species ~ ., data = iris)
Parameters:
SVM-Type: C-classification
SVM-Kernel: radial
cost: 1
gamma: 0.25
Number of Support Vectors: 51
( 8 22 21 )
Number of Classes: 3
Levels:
setosa versicolor virginica
通过summary函数可以得到关于模型的相关信息。
- 其中,SVM-Type项目说明本模型的类别为C分类器模型;
- SVM-Kernel项目说明本模型所使用的核函数为高斯内积函数且核函数中参数gamma的取值为0.25;
- cost项目说明本模型确定的约束违反成本为1;
- 此外我们可以看到,模型找到了51个支持向量:第一类包含有8个支持向量,第二类包含有22个支持想想,第三类包含21个支持向量。
- 最后一行说明模型中的三个类别分别为setosa、versicolor和virginica。
第二种使用svm()函数的方式则是根据所给的数据建立模型。这种方式形式要复杂一些,但是它允许我们以一种更加灵活的方式来构建模型。它的函数使用格式如下(注意我们仅列出了其中的主要参数)。
svm(x, y = NULL, scale = TRUE, type = NULL, kernel = "radial", degree = 3, gamma = if (is.vector(x)) 1 else 1 / ncol(x), coef0 = 0, cost = 1, nu = 0.5, subset, na.action = na.omit)
其中:
- x可以是一个数据矩阵,也可以是一个数据向量,同时也可以是一个稀疏矩阵。y是对于x数据的结果标签,它既可以是字符向量也可以为数值向量。x和y共同决定了将要用来建模的训练数据以及模型的积分形式。
- 参数type用于指定建立模型的类别。支持向量机模型通常可以用作分类模型、回归模型和异常检查模型。根据用途的不同,在svm函数中的type可取的值为C-classification、nu-classification、one-classification、eps-regression和nu-regression这五种类型。其中前三种是针对于字符结果变量的分类方式,其中第三种方式为逻辑判别,即判别结果输出所需判别样本是否属于该类别。而后两种则是针对数值型结果变量的分类方式。
- kernel是指在模型的建立过程中使用的核函数。针对线性不可分的问题,为了提高模型预测精度,通常会只用核函数对原始数据进行变换,提高原始特征维度,解决支持向量机模型线性不可分的问题。svm函数中kernel参数有四个可选核函数,分别为线性核函数、多项式核函数、高斯核函数及神经网络核函数。其中,高斯核函数与多项式核函数被认为是性能最好、也是最常用的核函数。
核函数有两种主要类型:局部性核函数和全局性核函数,高斯核函数是一个典型的局部性核函数,而多项式核函数则是一个典型的全局性核函数。局部性核函数仅仅在测试点附近小邻域内对数据点有影响,其学习能力强,泛化性能较弱;而全局性核函数则相对来说泛化性能较强,学习能力较弱。
- 对于选定的核函数,degree参数是指核函数多项式内积函数中的参数,其默认值为3。gamma参数给出了一个核函数中除线性内积函数以外的所有函数的参数,默认值为1.coef0参数是指核函数中多项式内积函数sigmoid内积函数的中的参数,默认值为0.
- 参数cost是软间隔模型中离群点权重。
- 最后,参数nu是用于nu-regression、nu-classification和one-classification类型中的参数。
一个经验性的结论为,在利用svm函数建立支持向量机模型时,使用标准化后的数据建立的模型效果更好。根据函数的第二种使用格式,在针对上述数据建立模型时,首先应该将结果变量和特征变量分别提取出来。结果向量用一个向量表示,特征向量用一个矩阵表示。在确定好数据后还应根据数据分析所使用的核函数以及核函数所对应的参数值,通常默认使用高斯内积函数作为核函数。下面给出一段实例代码:
# 提取iris数据集中除第五列以外的数据作为特征变量
x <- iris[, -5]
# 提取iris数据集中第五列数据作为结果变量
y <- iris[, 5]
model3 <- svm(x, y, kernel = "radial",
gamma = if (is.vector(x)) 1 else 1 / ncol(x))
在使用第二种格式建立模型时,不需要特别强调所建立模型的形式,函数会自动将所有输入的特征变量数据作为建立模型所需要的特征向量。在上述过程中,确定核函数的gamma系数时所使用的代码代表的意思为:如果特征向量是向量则gamma值取1,否则gamma值为特征向量个数的倒数。
在利用样本数据建立模型之后,我们便可以利用模型来进行相应的预测和判别。基于svm函数建立的模型来进行预测时,可以选用函数predict函数来完成相应的工作。在使用该函数时,应该首先确认将要用于预测的样本数据,并将样本数据的特征变量整合后放入同一个矩阵。代码如下:
pred <- predict(model3, x) table(pred, y)
输出结果:
> pred <- predict(model3, x)
> table(pred, y)
y
pred setosa versicolor virginica
setosa 50 0 0
versicolor 0 48 2
virginica 0 2 48
通常在进行预测之后,还需要检查模型预测的准确程度,这时便需要使用函数table来对预测结果和真实结果做出对比展示。从上述代码的输出中,可以看到在模型预测时,模型将所有属于setosa类型的鸢尾花全部预测正确;模型将数据versicolor类型的鸢尾花中有48朵预测正确,另外两朵错误的预测为virginica类型;同样,模型将属于virginica类型的鸢尾花中的48朵预测正确,但也将另外两朵错误的预测为versicolor类型。
函数predict中的一个可选参数是decision.values,在默认情况下,该参数的缺省值为FALSE。若将其值置为TRUE,那么函数的返回值中将包含有一个名为decision.values的属性,该属性是一个n*c的矩阵。这里,n是被预测的数据量,c是一个二分类器的决策值。注意,因为我们使用支持向量机对样本数据进行分类,分类结果可能是有k个类别。那么这k个类别中任意两类之间都会有一个二分类器。所以,我么可以推断出总共的二分类器数量为K(k-1)/2。决策值矩阵中的列名就是二分类器的标签。代码如下:
pred <- predict(model3, x, decision.values = TRUE) attr(pred, "decision.values")[1:4, ]
输出如下:
> pred <- predict(model3, x, decision.values = TRUE)
> attr(pred, "decision.values")[1:4, ]
setosa/versicolor setosa/virginica
1 1.196152 1.091757
2 1.064621 1.056185
3 1.180842 1.074542
4 1.110699 1.053012
versicolor/virginica
1 0.6708810
2 0.8483518
3 0.6439798
4 0.6782041
由于我们处理的是一个分类问题。所以分类决策最终是经由一个sign()函数来完成的。从上面的输出中可以看到,对于样本数据4而言,标签setosa/versicolor对应的值大于0,因此属于setosa类;标签setosa/virginica对应的值同样大于0,因此数据setosa类;在二分类器versicolor/virginica中对应的决策值大于0,判定属于versicolor类。所以,最终样本数据4被判定数据setosa类。
可视化模型,代码如下:
> plot(cmdscale(dist(iris[,-5])),
+ col=c("orange", "blue", "green")[as.integer(iris[,5])],
+ pch=c("o", "+")[1:150 %in% model3$index + 1])
>
> # ?legend
> legend(1.8, -0.5, c("setosa","versicolor", "virgincia"),
+ col = c("orange","blue","green"), lty = 1,
+ cex = 0.6,
+ bty = "o", box.lty = 1, box.col = "black")

在图中我们可以看到,鸢尾花中的第一种setosa类别同其他两种区别较大,而剩下的versicolor类别和virginica类别却相差很小,甚至存在交叉难以区分。注意,这是在使用了全部四种特征之后仍然难以区分的。这也从另一个角度解释了在模型预测过程中出现的问题,所以模型误将2朵versicolor 类别的花预测成了virginica 类别,而将2朵virginica 类别的花错误地预测成了versicolor 类别,也就是很正常现象了。
到此这篇关于R语言实现支持向量机SVM应用案例的文章就介绍到这了,更多相关R语言支持向量机SVM内容请搜索服务器之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持服务器之家!
原文链接:https://blog.csdn.net/yitian_z/article/details/103097463