数据结构平衡二叉树
参考代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
|
/* 名称:平衡二叉树 语言:数据结构C语言版 编译环境:VC++ 6.0 日期: 2014-3-26 */#include <stdio.h> #include <malloc.h> #include <windows.h> #define LH +1 // 左高 #define EH 0 // 等高 #define RH -1 // 右高 #define N 5 // 数据元素个数 typedef char KeyType; // 设关键字域为字符型 typedef struct{ KeyType key; int order; }ElemType; // 数据元素类型 // 平衡二叉树的类型 typedef struct BSTNode { ElemType data; // bf结点的平衡因子,只能够取0,-1,1,它是左子树的深度减去 // 右子树的深度得到的 int bf; struct BSTNode *lchild,*rchild; // 左、右孩子指针 }BSTNode,*BSTree; // 构造一个空的动态查找表DT int InitDSTable(BSTree *DT) { *DT=NULL; return 1; } // 销毁动态查找表DT void DestroyDSTable(BSTree *DT) { if(*DT) // 非空树 { if((*DT)->lchild) // 有左孩子 DestroyDSTable(&(*DT)->lchild); // 销毁左孩子子树 if((*DT)->rchild) // 有右孩子 DestroyDSTable(&(*DT)->rchild); // 销毁右孩子子树 free(*DT); // 释放根结点 *DT=NULL; // 空指针赋0 } } // 在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素, // 若查找成功,则返回指向该数据元素结点的指针,否则返回空指针。 BSTree SearchBST(BSTree T,KeyType key) { if((!T)|| (key == T->data.key)) return T; // 查找结束 else if(key < T->data.key) // 在左子树中继续查找 return SearchBST(T->lchild,key); else return SearchBST(T->rchild,key); // 在右子树中继续查找 } // 对以*p为根的二叉排序树作右旋处理,处理之后p指向新的树根结点,即旋转 // 处理之前的左子树的根结点。 void R_Rotate(BSTree *p) { BSTree lc; lc=(*p)->lchild; // lc指向p的左子树根结点 (*p)->lchild=lc->rchild; // lc的右子树挂接为p的左子树 lc->rchild=*p; *p=lc; // p指向新的根结点 } // 对以*p为根的二叉排序树作左旋处理,处理之后p指向新的树根结点,即旋转 // 处理之前的右子树的根结点。 void L_Rotate(BSTree *p) { BSTree rc; rc=(*p)->rchild; // rc指向p的右子树根结点 (*p)->rchild=rc->lchild; // rc的左子树挂接为p的右子树 rc->lchild=*p; *p=rc; // p指向新的根结点 } // 对以指针T所指结点为根的二叉树作左平衡旋转处理,本算法结束时, // 指针T指向新的根结点。 void LeftBalance(BSTree *T) { BSTree lc,rd; lc=(*T)->lchild; // lc指向*T的左子树根结点 switch(lc->bf) { // 检查*T的左子树的平衡度,并作相应平衡处理 case LH: // 新结点插入在*T的左孩子的左子树上,要作单右旋处理 (*T)->bf=lc->bf=EH; R_Rotate(T); break; case RH: // 新结点插入在*T的左孩子的右子树上,要作双旋处理 rd=lc->rchild; // rd指向*T的左孩子的右子树根 switch(rd->bf) { // 修改*T及其左孩子的平衡因子 case LH: (*T)->bf=RH; lc->bf=EH; break; case EH: (*T)->bf=lc->bf=EH; break; case RH: (*T)->bf=EH; lc->bf=LH; } rd->bf=EH; L_Rotate(&(*T)->lchild); // 对*T的左子树作左旋平衡处理 R_Rotate(T); // 对*T作右旋平衡处理 } } // 对以指针T所指结点为根的二叉树作右平衡旋转处理,本算法结束时, // 指针T指向新的根结点 void RightBalance(BSTree *T) { BSTree rc,rd; rc=(*T)->rchild; // rc指向*T的右子树根结点 switch(rc->bf) { // 检查*T的右子树的平衡度,并作相应平衡处理 case RH: // 新结点插入在*T的右孩子的右子树上,要作单左旋处理 (*T)->bf=rc->bf=EH; L_Rotate(T); break; case LH: // 新结点插入在*T的右孩子的左子树上,要作双旋处理 rd=rc->lchild; // rd指向*T的右孩子的左子树根 switch(rd->bf) { // 修改*T及其右孩子的平衡因子 case RH: (*T)->bf=LH; rc->bf=EH; break; case EH: (*T)->bf=rc->bf=EH; break; case LH: (*T)->bf=EH; rc->bf=RH; } rd->bf=EH; R_Rotate(&(*T)->rchild); // 对*T的右子树作右旋平衡处理 L_Rotate(T); // 对*T作左旋平衡处理 } } // 若在平衡的二叉排序树T中不存在和e有相同关键字的结点,则插入一个 // 数据元素为e的新结点,并返回1,否则返回0。若因插入而使二叉排序树 // 失去平衡,则作平衡旋转处理,布尔变量taller反映T长高与否。 int InsertAVL(BSTree *T,ElemType e,int *taller) { if(!*T) { // 插入新结点,树“长高”,置taller为1 *T=(BSTree)malloc(sizeof(BSTNode)); (*T)->data=e; (*T)->lchild=(*T)->rchild=NULL; (*T)->bf=EH; *taller=1; } else { if(e.key == (*T)->data.key) { // 树中已存在和e有相同关键字的结点则不再插入 *taller=0; return 0; } if(e.key < (*T)->data.key) { // 应继续在*T的左子树中进行搜索 if(!InsertAVL(&(*T)->lchild,e,taller)) // 未插入 return 0; if(*taller) // 已插入到*T的左子树中且左子树“长高” switch((*T)->bf) // 检查*T的平衡度 { case LH: // 原本左子树比右子树高,需要作左平衡处理 LeftBalance(T); *taller=0; //标志没长高 break; case EH: // 原本左、右子树等高,现因左子树增高而使树增高 (*T)->bf=LH; *taller=1; //标志长高 break; case RH: // 原本右子树比左子树高,现左、右子树等高 (*T)->bf=EH; *taller=0; //标志没长高 } } else { // 应继续在*T的右子树中进行搜索 if(!InsertAVL(&(*T)->rchild,e,taller)) // 未插入 return 0; if(*taller) // 已插入到T的右子树且右子树“长高” switch((*T)->bf) // 检查T的平衡度 { case LH: (*T)->bf=EH; // 原本左子树比右子树高,现左、右子树等高 *taller=0; break; case EH: // 原本左、右子树等高,现因右子树增高而使树增高 (*T)->bf=RH; *taller=1; break; case RH: // 原本右子树比左子树高,需要作右平衡处理 RightBalance(T); *taller=0; } } } return 1; } // 按关键字的顺序对DT的每个结点调用函数Visit()一次 void TraverseDSTable(BSTree DT,void(*Visit)(ElemType)) { if(DT) { TraverseDSTable(DT->lchild,Visit); // 先中序遍历左子树 Visit(DT->data); // 再访问根结点 TraverseDSTable(DT->rchild,Visit); // 最后中序遍历右子树 } } void print(ElemType c) { printf("(%d,%d)",c.key,c.order); } int main() { BSTree dt,p; int k; int i; KeyType j; ElemType r[N]={ {13,1},{24,2},{37,3},{90,4},{53,5} }; // (以教科书P234图9.12为例) InitDSTable(&dt); // 初始化空树 for(i=0;i<N;i++) InsertAVL(&dt,r[i],&k); // 建平衡二叉树 TraverseDSTable(dt,print); // 按关键字顺序遍历二叉树 printf("\n请输入待查找的关键字: "); scanf("%d",&j); p=SearchBST(dt,j); // 查找给定关键字的记录 if(p) print(p->data); else printf("表中不存在此值"); printf("\n"); DestroyDSTable(&dt); system("pause"); return 0; } /* 输出效果: (13,1)(24,2)(37,3)(53,5)(90,4) 请输入待查找的关键字: 53 (53,5) 请按任意键继续. . . */ |
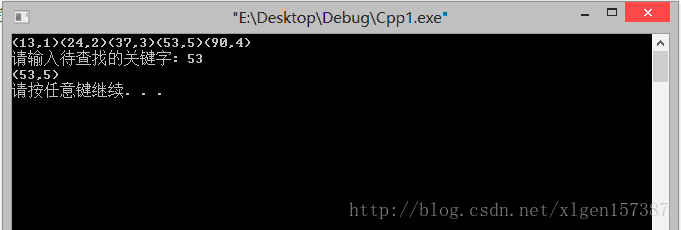
运行结果如下:
感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!
原文链接:http://blog.csdn.net/xlgen157387/article/details/22169107