本文详细讲述了C++实现二叉树遍历序列的求解方法,对于数据结构与算法的学习有着很好的参考借鉴价值。具体分析如下:
一、由遍历序列构造二叉树
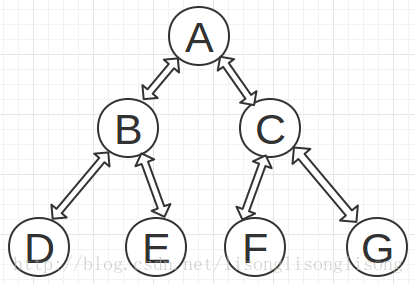
如上图所示为一个二叉树,可知它的遍历序列分别为:
先序遍历:ABDECFG
中序遍历:DBEAFCG
后序遍历:DEBFGCA
我们需要知道的是,由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树;由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树;但是如果只知道先序序列和后序序列,则无法唯一确定一棵二叉树。
二、已知二叉树的先序序列和中序序列,求后序序列。
因为由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树,所以进而可以唯一地确定它的后序遍历。在先序遍历序列中,第一个结点一定是二叉树的根结点,而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列就是左子树的中序序列,后一个子序列就是右子树的中序序列。根据这两个子序列的长度,可以在先序序列中找到对应的左子树先序序列和右子树先序序列。而左子树先序序列的第一个结点是左子树的根结点,右子树先序序列的第一个结点是右子树的根结点。如此递归地进行下去,便能唯一地确定这棵二叉树。
C++实现代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
/************************************************************************* > File Name: Test.cpp > Author: SongLee ************************************************************************/#include<iostream>using namespace std;struct TreeNode{ struct TreeNode* left; struct TreeNode* right; char elem;};TreeNode* PostOrderFromOrderings(char* inorder, char* preorder, int length){ if(length == 0) { return NULL; } TreeNode* node = new TreeNode; node->elem = *preorder; int rootIndex = 0; for(; rootIndex < length; rootIndex++) // 求左子树的长度 { if(inorder[rootIndex] == *preorder) break; } node->left = PostOrderFromOrderings(inorder, preorder + 1, rootIndex); node->right = PostOrderFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1)); cout << node->elem << " "; // 求后序序列,所以最后输出根结点 return node;}int main(){ char* pre = "ABDECFG"; char* in = "DBEAFCG"; PostOrderFromOrderings(in, pre, 7); cout << endl; return 0;} |
三、已知二叉树的后序序列和中序序列,求先序序列。
同理,由二叉树的后序序列和中序序列也可以唯一地确定一棵二叉树,所以进而可以唯一地确定先序遍历序列。因为后序序列的最后一个结点就如同先序序列的第一个结点,可以将中序序列分割成两个子序列,然后采用类似的方法递归地进行划分。
C++实现代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
/************************************************************************* > File Name: Test1.cpp > Author: SongLee ************************************************************************/#include<iostream>using namespace std;struct TreeNode{ struct TreeNode* left; struct TreeNode* right; char elem;};TreeNode* PreOrderFromOrderings(char* inorder, char* postorder, int length){ if(length == 0) { return NULL; } TreeNode* node = new TreeNode; node->elem = postorder[length-1]; int rootIndex = 0; for(; rootIndex < length; rootIndex++) // 求左子树的长度 { if(inorder[rootIndex] == postorder[length-1]) break; } cout << node->elem << " "; // 求先序序列,所以先输出根结点 node->left = PreOrderFromOrderings(inorder, postorder, rootIndex); node->right = PreOrderFromOrderings(inorder + rootIndex + 1, postorder + rootIndex, length - (rootIndex + 1)); return node;}int main(){ char* post = "DEBFGCA"; char* in = "DBEAFCG"; PreOrderFromOrderings(in, post, 7); cout << endl; return 0;} |
相信本文所述实例对于大家学习数据结构与算法会起到一定的帮助作用。














