本文实例讲述了Python实现螺旋矩阵的填充算法。分享给大家供大家参考,具体如下:
afanty的分析:
关于矩阵(二维数组)填充问题自己动手推推,分析下两个下表的移动规律就很容易咯。
对于螺旋矩阵,不管它是什么鬼,反正就是依次向右、向下、向右、向上移动。
向右移动:横坐标不变,纵坐标加1
向下移动:纵坐标不变,横坐标加1
向右移动:横坐标不变,纵坐标减1
向上移动:纵坐标不变,横坐标减1
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#coding=utf-8import numpy'''''Author: afantyDate: 2016/6/23'''def helixMatrix(n): '''''实现n维螺旋矩阵的填充 :param n:维数 :return:螺旋矩阵 ''' if not isinstance(n, int) or n <= 0: raise ValueError('请输入合适的维数') matrix = numpy.zeros((n, n)) left_top = 0 right_buttom = n - 1 number = 1 while left_top < right_buttom: # 向右移动,横坐标不变,纵坐标+1,number+1 i = left_top while i < right_buttom: matrix[left_top][i] = number i += 1 number += 1 # while # 向下移动,纵坐标不变,横坐标+1,number+1 i = left_top while i < right_buttom: matrix[i][right_buttom] = number i += 1 number += 1 #while # 向左移动,横坐标不变,纵坐标-1,number+1 i = right_buttom while i > left_top: matrix[right_buttom][i] = number i -= 1 number += 1 # while # 向上移动,纵坐标不变,横坐标-1,number+1 i = right_buttom while i > left_top: matrix[i][left_top] = number i -= 1 number += 1 # while left_top += 1 right_buttom -= 1 # while if n % 2 != 0: matrix[n / 2][n / 2] = n * n return matrix# endprint("服务器之家测试结果:")print helixMatrix(5) |
运行结果:
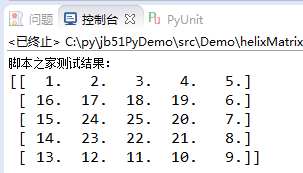
希望本文所述对大家Python程序设计有所帮助。
原文链接:http://blog.csdn.net/mo_yihua/article/details/51743722










