二叉树(binary tree)是一颗树,其中每个节点都不能有多于两个的儿子。
1.二叉树节点
作为图的特殊形式,二叉树的基本组成单元是节点与边;作为数据结构,其基本的组成实体是二叉树节点(binary tree node),而边则对应于节点之间的相互引用。
如下,给出了二叉树节点的数据结构图示和相关代码:

|
1
2
3
4
5
6
7
8
9
10
11
12
|
// 定义节点类:private static class binnode { private object element; private binnode lchild;// 定义指向左子树的指针 private binnode rchild;// 定义指向右子树的指针 public binnode(object element, binnode lchild, binnode rchild) { this.element = element; this.lchild = lchild; this.rchild = rchild; }} |
2.递归遍历
二叉树本身并不具有天然的全局次序,故为实现遍历,需通过在各节点与其孩子之间约定某种局部次序,间接地定义某种全局次序。
按惯例左兄弟优先于右兄弟,故若将节点及其孩子分别记作v、l和r,则下图所示,局部访问的次序可有vlr、lvr和lrv三种选择。根据节点v在其中的访问次序,三种策略也相应地分别称作先序遍历、中序遍历和后序遍历,下面将分别介绍。

2.1 先序遍历
图示:
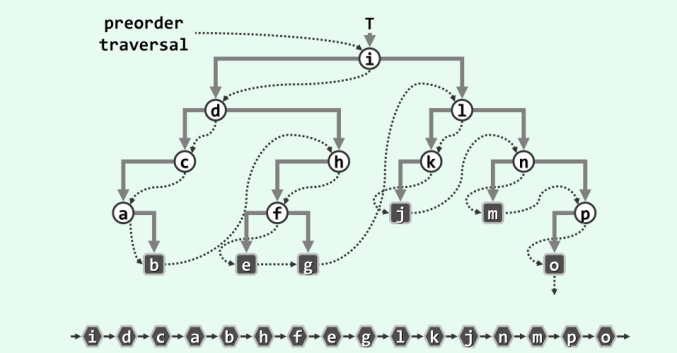
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
/** * 对该二叉树进行前序遍历 结果存储到list中 前序遍历 */public static void preorder(binnode node) { list.add(node); // 先将根节点存入list // 如果左子树不为空继续往左找,在递归调用方法的时候一直会将子树的根存入list,这就做到了先遍历根节点 if (node.lchild != null) { preorder(node.lchild); } // 无论走到哪一层,只要当前节点左子树为空,那么就可以在右子树上遍历,保证了根左右的遍历顺序 if (node.rchild != null) { preorder(node.rchild); }} |
2.2 中序遍历
图示:
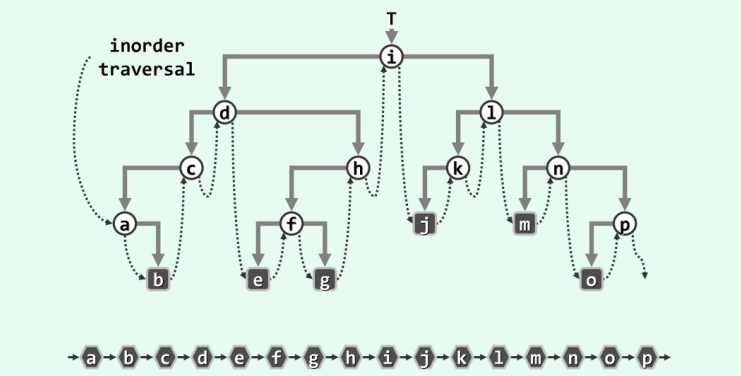
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
/** * 对该二叉树进行中序遍历 结果存储到list中 */public static void inorder(binnode node) { if (node.lchild != null) { inorder(node.lchild); } list.add(node); if (node.rchild != null) { inorder(node.rchild); }} |
2.3 后序遍历
实例图示:
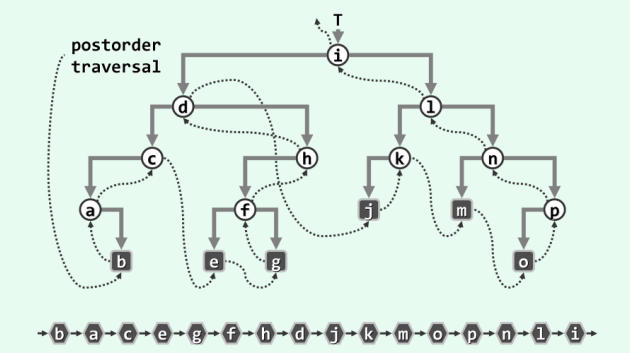
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
/** * 对该二叉树进行后序遍历 结果存储到list中 */public static void postorder(binnode node) { if (node.lchild != null) { postorder(node.lchild); } if (node.rchild != null) { postorder(node.rchild); } list.add(node);} |
附:测试相关代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
private static binnode root;private static list<binnode> list = new arraylist<binnode>();public static void main(string[] args) { init(); // todo auto-generated method stub //preorder(root); //inorder(root); postorder(root); for (int i = 0; i < list.size(); i++) { system.out.print(list.get(i).element + " "); }}// 树的初始化:先从叶节点开始,由叶到根public static void init() { binnode b = new binnode("b", null, null); binnode a = new binnode("a", null, b); binnode c = new binnode("c", a, null); binnode e = new binnode("e", null, null); binnode g = new binnode("g", null, null); binnode f = new binnode("f", e, g); binnode h = new binnode("h", f, null); binnode d = new binnode("d", c, h); binnode j = new binnode("j", null, null); binnode k = new binnode("k", j, null); binnode m = new binnode("m", null, null); binnode o = new binnode("o", null, null); binnode p = new binnode("p", o, null); binnode n = new binnode("n", m, p); binnode l = new binnode("l", k, n); root = new binnode("i", d, l);} |
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://www.jianshu.com/p/f0a6d594711d















