Torch.stack()
1. 概念
在一个新的维度上连接一个张量序列
2. 参数
- tensors (sequence)需要连接的张量序列
- dim (int)在第dim个维度上连接
注意输入的张量shape要完全一致,且dim必须小于len(tensors)。
3. 举例
3.1 四个shape为[3, 3]的张量
a = torch.Tensor([[1,2,3],[4,5,6],[7,8,9]])
b = torch.Tensor([[10,20,30],[40,50,60],[70,80,90]])
c = torch.Tensor([[100,200,300],[400,500,600],[700,800,900]])
d = torch.Tensor([[1000,2000,3000],[4000,5000,6000],[7000,8000,9000]])
以下面这4个张量,每个张量shape为[3, 3]。
3.1.1 dim=0的情况下,直接来看结果。
torch.stack((a,b,c,d),dim=0)

此时在第0个维度上连接,新张量的shape可以发现为[4, 3, 3],4代表在第0个维度有4项。
观察可以得知:即初始的四个张量,即a、b、c、d四个初始张量。
可以理解为新张量的第0个维度上连接a、b、c、d。
3.1.2 dim=1的情况下
torch.stack((a,b,c,d),dim=1)
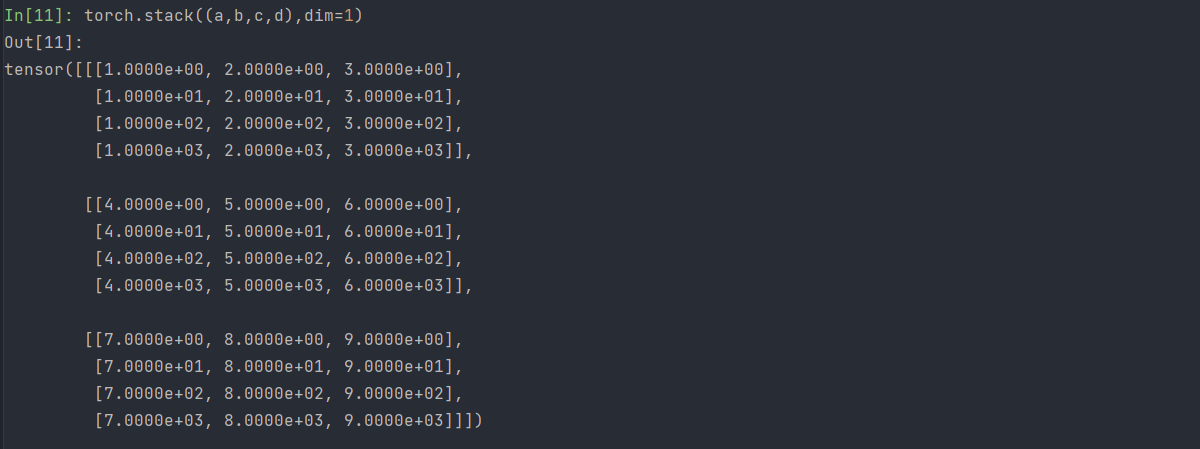
此时在第1个维度上连接,新张量的shape可以发现为[3,4, 3],4代表在第1个维度有4项。
观察可以得知:
- 新张量[0][0]为a[0],[0][1]为b[0],[0][2]为c[0],[0][3]为d[0]
- 新张量[1][0]为a[1],[1][1]为b[1],[1][2]为c[1],[1][3]为d[1]
- 新张量[2][0]为a[2],[2][1]为b[2],[2][2]为c[2],[2][3]为d[2]
可以理解为新张量的第1个维度上连接a、b、c、d的第0个维度单位,具体地说,在新张量[i]中连接a[i]、b[i]、c[i]、d[i],即将a[i]赋给新张量[i][0]、b[i]赋给新张量[i][1]、c[i]赋给新张量[i][2]、d[i]赋给新张量[i][3]。
3.1.2 dim=2的情况下

此时在第2个维度上连接,新张量的shape可以发现为[3,3,4],4代表在第2个维度有4项。
观察可以得知:
新张量[0][0][0]为a[0][0],[0][0][1]为b[0][0],[0][0][2]为c[0][0],[0][0][3]为d[0][0]
新张量[0][1][0]为a[0][1],[0][1][1]为b[0][1],[0][1][2]为c[0][1],[0][1][3]为d[0][1]
新张量[0][2][0]为a[0][2],[0][2][1]为b[0][2],[0][2][2]为c[0][2],[0][2][3]为d[0][2]
新张量[1][0][0]为a[1][0],[1][0][1]为b[1][0],[1][0][2]为c[1][0],[1][0][3]为d[1][0]
新张量[1][1][0]为a[1][1],[1][1][1]为b[1][1],[1][1][2]为c[1][1],[1][1][3]为d[1][1]
新张量[1][2][0]为a[1][2],[1][2][1]为b[1][2],[1][2][2]为c[1][2],[1][2][3]为d[1][2]
新张量[2][0][0]为a[2][0],[2][0][1]为b[2][0],[2][0][2]为c[2][0],[2][0][3]为d[2][0]
新张量[2][1][0]为a[2][1],[2][1][1]为b[2][1],[2][1][2]为c[2][1],[2][1][3]为d[2][1]
新张量[2][2][0]为a[2][2],[2][2][1]为b[2][2],[2][2][2]为c[2][2],[2][2][3]为d[2][2]
可以理解为新张量的第2个维度上连接a、b、c、d的第1个维度的单位,具体地说,在新张量[i][j]中连接a[i][j]、b[i][j]、c[i][j]、d[i][]j。
3.1.3 总结
通过dim=0、1、2的情况,可以总结并推涨出规律:
假设有n个[x,y]的张量,当dim=z时。新张量在第z个维度上连接n个张量第z-1维度的单位,具体来说,新张量[i][i+1]..[i+z-1]中依次连接n个向量[i][i+1]..[i+z-1]。
3.2 7个shape为[5, 7, 4, 2]的张量
a1 = torch.rand([5, 7, 4, 3])
a2 = a1 + 1
a3 = a2 + 1
a4 = a3 + 1
a5 = a4 + 1
a6 = a5 + 1
a7 = a6 + 1
假设dim=3时连接
test = torch.stack((a1, a2, a3, a4, a5, a6, a7), dim=3)
7个张量在第3个维度连接后形成的新张量赋为test,test的shape为[5, 7, 4,7, 3],代表在第3个维度有7项。
随机(在新张量[0][0][0]到新张量[4][6][3]区间内)查看一个新张量第3维度上的单位:
a = test[0][1][2]

再根据总结的规律,将7个向量中的[0][1][2]连接起来,再次查看,验证了规律。
b = torch.zeros(0)
for i in (a1, a2, a3, a4, a5, a6, a7):
b = torch.cat((b, i[0][1][2]), dim=0)

4. 理解
通过shape来看,假设shape为[a, b, c... z],有n个shape相同的张量,在dim=x时连接n个张量,可以得到新张量,shape为[a, b, c, ... n, ...z],其中n所在维度即为第x个维度。
然后即可通过新张量[i][i+1]..[i+x-1]看作索引,对应的数据为n个张量[i][i+1][i+x-1]按顺序连接。
到此这篇关于Pytorch中stack()方法的总结及理解的文章就介绍到这了,更多相关Pytorch中stack()方法的总结及理解内容请搜索服务器之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持服务器之家!
原文链接:https://www.cnblogs.com/tangzj/p/15526544.html










