本篇接上一篇:python算法学习双曲嵌入论文代码实现数据集介绍
1. 方法说明
首先学习相关的论文中的一些知识,并结合进行代码的编写。文中主要使用Poincaré embedding。

对应的python代码为:
|
1
2
3
|
def dist1(vec1, vec2): # eqn1 diff_vec = vec1 - vec2 return 1 + 2 * norm(diff_vec) / ((1 - norm(vec1)) * (1 - norm(vec2))) |

损失函数
我们想要寻找最优的embedding,就需要构建一个损失函数,目标是使得相似词汇的embedding结果,尽可能接近,且层级越高(类别越大)的词越靠近中心。我们需要最小化这个损失函数,从而得到embedding的结果。

其实在传统的词嵌入中,我们也是用上述的损失函数,但距离选用的是余弦距离。
梯度下降
后面将使用梯度下降方法进行求解迭代。
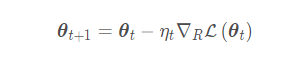
由于是将欧氏空间计算得到的梯度在黎曼空间中进行迭代,由上文的(1)式,我们有:
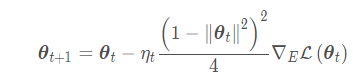
梯度求解
202111595310129

对应的更新函数在Python中设置如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
# 范数计算def norm(x): return np.dot(x, x)# 距离函数对\theta求偏导def compute_distance_gradients(theta, x, gamma): alpha = (1.0 - np.dot(theta, theta)) norm_x = norm(x) beta = (1 - norm_x) c_ = 4.0 / (alpha * beta * sqrt(gamma ** 2 - 1)) return c_ * ((norm_x - 2 * np.dot(theta, x) + 1) / alpha * theta - x)# 更新公式def update(emb, grad, lr): c_ = (1 - norm(emb)) ** 2 / 4 upd = lr * c_ * grad emb = emb - upd if (norm(emb) >= 1): emb = emb / sqrt(norm(emb)) - eps return emb |
至此,我们就可以开始写一个完整的训练过程了。在这之前,再补充一个绘图函数(可以看embedding的实际训练情况):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def plotall(ii): fig = plt.figure(figsize=(10, 10)) # 绘制所有节点 for a in emb: plt.plot(emb[a][0], emb[a][1], marker = 'o', color = [levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1)]) for a in network: for b in network[a]: plt.plot([emb[a][0], emb[b][0]], [emb[a][1], emb[b][1]], color = [levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1),levelOfNode[a]/(last_level+1)]) circle = plt.Circle((0, 0), 1, color='y', fill=False) plt.gcf().gca().add_artist(circle) plt.xlim(-1, 1) plt.ylim(-1, 1) fig.savefig('~/GitHub/hyperE/fig/' + str(last_level) + '_' + str(ii) + '.png', dpi = 200) |
2. 代码训练过程
首先初始化embeddings,这里按照论文中写的,用 ( − 0.001 , 0.001 ) (-0.001, 0.001) (−0.001,0.001)间的均匀分布进行随机初始化:
|
1
2
3
|
emb = {}for node in levelOfNode: emb[node] = np.random.uniform(low = -0.001, high = 0.001, size = (2, )) |
下面设置学习率等参数:
|
1
2
3
4
|
vocab = list(emb.keys())eps = 1e-5 lr = 0.1 # 学习率num_negs = 10 # 负样本个数 |
接下来开始正式迭代,具体每一行的含义均在注释中有进行说明:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
# 绘制初始化权重plotall("init")for epoch in range(1000): loss = [] random.shuffle(vocab) # 下面需要抽取不同的样本:pos2 与 pos1 相关;negs 不与 pos1 相关 for pos1 in vocab: if not network[pos1]: # 叶子节点则不进行训练 continue pos2 = random.choice(network[pos1]) # 随机选取与pos1相关的节点pos2 dist_pos_ = dist1(emb[pos1], emb[pos2]) # 保留中间变量gamma,加速计算 dist_pos = np.arccosh(dist_pos_) # 计算pos1与pos2之间的距离 # 下面抽取负样本组(不与pos1相关的样本组) negs = [[pos1, pos1]] dist_negs_ = [1] dist_negs = [0] while (len(negs) < num_negs): neg = random.choice(vocab) # 保证负样本neg与pos1没有边相连接 if not (neg in network[pos1] or pos1 in network[neg] or neg == pos1): dist_neg_ = dist1(emb[pos1], emb[neg]) dist_neg = np.arccosh(dist_neg_) negs.append([pos1, neg]) dist_negs_.append(dist_neg_) # 保存中间变量gamma,加速计算 dist_negs.append(dist_neg) # 针对一个样本的损失 loss_neg = 0.0 for dist_neg in dist_negs: loss_neg += exp(-1 * dist_neg) loss.append(dist_pos + log(loss_neg)) # 损失函数 对 正样本对 距离 d(u, v) 的导数 grad_L_pos = -1 # 损失函数 对 负样本对 距离 d(u, v') 的导数 grad_L_negs = [] for dist_neg in dist_negs: grad_L_negs.append(exp(-dist_neg) / loss_neg) # 计算正样本对中两个样本的embedding的更新方向 grad_pos1 = grad_L_pos * compute_distance_gradients(emb[pos1], emb[pos2], dist_pos_) grad_pos2 = grad_L_pos * compute_distance_gradients(emb[pos2], emb[pos1], dist_pos_) # 计算负样本对中所有样本的embedding的更新方向 grad_negs_final = [] for (grad_L_neg, neg, dist_neg_) in zip(grad_L_negs[1:], negs[1:], dist_negs_[1:]): grad_neg0 = grad_L_neg * compute_distance_gradients(emb[neg[0]], emb[neg[1]], dist_neg_) grad_neg1 = grad_L_neg * compute_distance_gradients(emb[neg[1]], emb[neg[0]], dist_neg_) grad_negs_final.append([grad_neg0, grad_neg1]) # 更新embeddings emb[pos1] = update(emb[pos1], -grad_pos1, lr) emb[pos2] = update(emb[pos2], -grad_pos2, lr) for (neg, grad_neg) in zip(negs, grad_negs_final): emb[neg[0]] = update(emb[neg[0]], -grad_neg[0], lr) emb[neg[1]] = update(emb[neg[1]], -grad_neg[1], lr) # 输出损失 if ((epoch) % 10 == 0): print(epoch + 1, "---Loss: ", sum(loss)) # 绘制二维embeddings if ((epoch) % 100 == 0): plotall(epoch + 1) |
3. 结果表现
结果如下所示(与论文有些不一致):
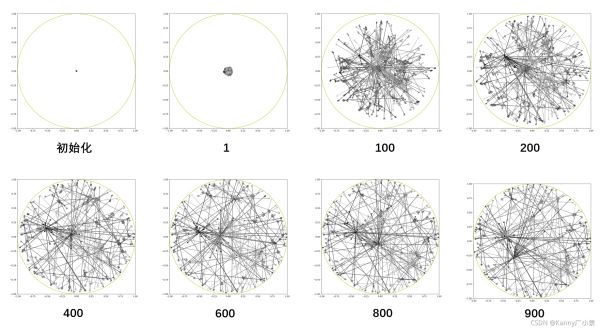
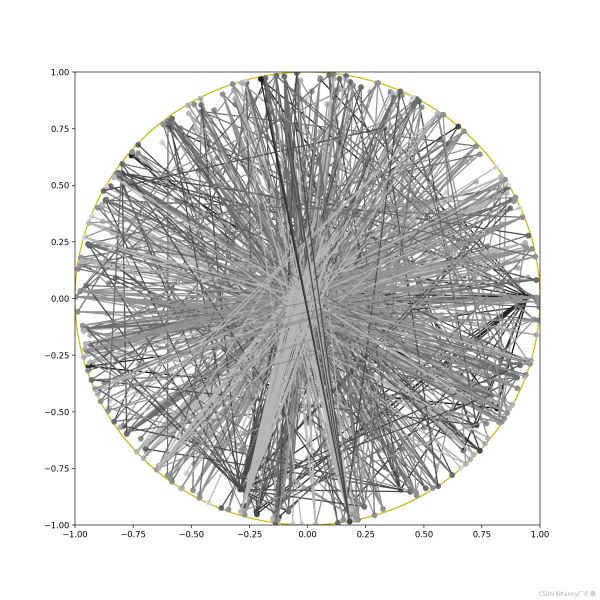
实际上应该还是有效的,有些团都能聚合在一起,下面是一个随机训练的结果(可以看出非常混乱):
其他参考资料
Poincaré Embeddings for Learning Hierarchical Representations
Implementing Poincaré Embeddings
models.poincare – Train and use Poincare embeddings
How to make a graph on Python describing WordNet's synsets (NLTK)
networkx.drawing.nx_pylab.draw_networkx
以上就是python算法学习双曲嵌入论文方法与代码解析说明的详细内容,更多关于python双曲嵌入论文方法与代码的资料请关注服务器之家其它相关文章!
原文链接:https://blog.csdn.net/weixin_41929524/article/details/121071272










