一、什么是集成学习
集成学习是一种技术框架,它本身不是一个单独的机器学习算法,而是通过构建并结合多个机器学习器来完成学习任务,一般结构是:先产生一组“个体学习器”,再用某种策略将它们结合起来,目前,有三种常见的集成学习框架(策略):bagging,boosting和stacking
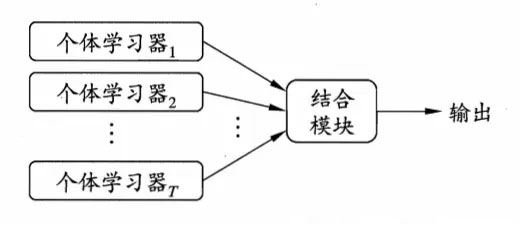
也就是说,集成学习有两个主要的问题需要解决,第一是如何得到若干个个体学习器,第二是如何选择一种结合策略,将这些个体学习器集合成一个强学习器
集成学习是指将若干弱分类器组合之后产生一个强分类器。弱分类器(weak learner)指那些分类准确率只稍好于随机猜测的分类器(error rate < 50%)。如今集成学习有两个流派,一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合,随机森林算法就属于bagging派系;另一个是boosting派系,它的特点是各个弱学习器之间有依赖关系,adaboost算法就属于boosting派系。在实现集成学习算法时,很重要的一个核心就是如何实现数据的多样性,从而实现弱分类器的多样性
集成学习有如下的特点:
(1)将多个分类方法聚集在一起,以提高分类的准确率(这些算法可以是不同的算法,也可以是相同的算法。);
(2)集成学习法由训练数据构建一组基分类器,然后通过对每个基分类器的预测进行投票来进行分类;
(3)严格来说,集成学习并不算是一种分类器,而是一种分类器结合的方法;
(4)通常一个集成分类器的分类性能会好于单个分类器;
(5)如果把单个分类器比作一个决策者的话,集成学习的方法就相当于多个决策者共同进行一项决策。
bagging和boosting的使用区别如下:
1)样本选择:
bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
2)样例权重
bagging:使用均匀取样,每个样例的权重相等
boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。
3)预测函数
bagging:所有预测函数的权重相等。
boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
4)并行计算
bagging:各个预测函数可以并行生成
boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
5)计算效果
bagging主要减小了variance,而boosting主要减小了bias,而这种差异直接推动结合bagging和boosting的multiboosting的诞生
二、bagging算法
bagging(装袋算法)的集成学习方法非常简单,假设我们有一个数据集d,使用bootstrap sample(有放回的随机采样,这里说明一下,有放回抽样是抽一个就放回一个,然后再抽,而不是这个人抽10个,再放回,下一个继续抽,它是每一个样本被抽中概率符合均匀分布)的方法取了k个数据子集(子集样本数都相等):d1,d2,…,dk,作为新的训练集,我们使用这k个子集分别训练一个分类器(使用分类、回归等算法),最后会得到k个分类模型。我们将测试数据输入到这k个分类器,会得到k个分类结果,比如分类结果是0和1,那么这k个结果中谁占比最多,那么预测结果就是谁。
大致过程如下:
1.对于给定的训练样本s,每轮从训练样本s中采用有放回抽样(booststraping)的方式抽取m个训练样本,共进行n轮,得到了n个样本集合,需要注意的是这里的n个训练集之间是相互独立的。
2.在获取了样本集合之后,每次使用一个样本集合得到一个预测模型,对于n个样本集合来说,我们总共可以得到n个预测模型。
3.如果我们需要解决的是分类问题,那么我们可以对前面得到的n个模型采用投票的方式得到分类的结果,对于回归问题来说,我们可以采用计算模型均值的方法来作为最终预测的结果。
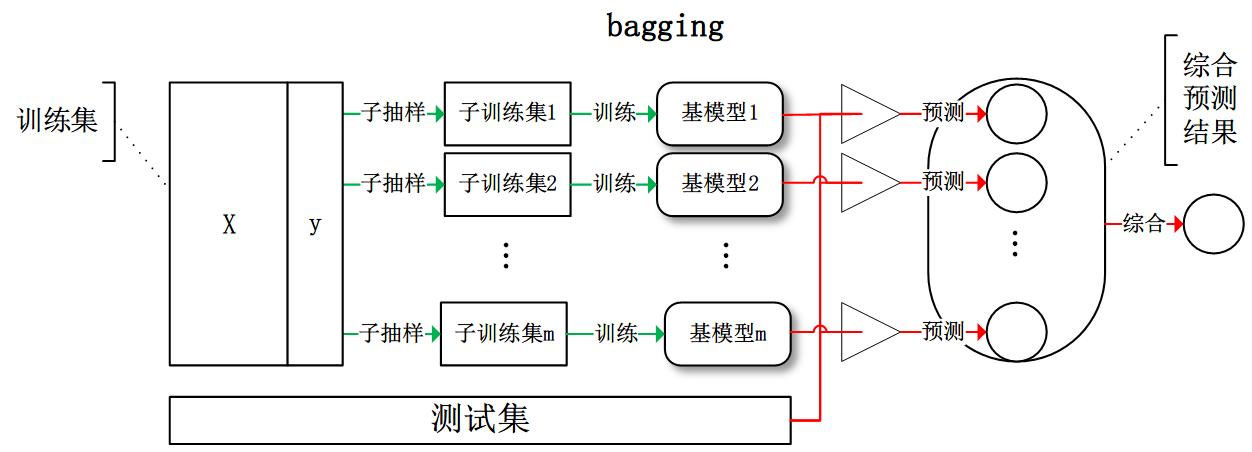
那么我们什么时候该使用bagging集成方法:学习算法不稳定:就是说如果训练集稍微有所改变就会导致分类器性能比较大大变化那么我们可以采用bagging这种集成方法adaboost只适用于二分类任务不同,bagging可以用于多分类,回归的任务举个例子可以看出bagging的好处:x 表示一维属性,y 表示类标号(1或-1)测试条件:当x<=k时,y=?;当x>k时,y=?;k为最佳分裂点下表为属性x对应的唯一正确的y类别:

每一轮随机抽样后,都生成一个分类器。然后再将五轮分类融合
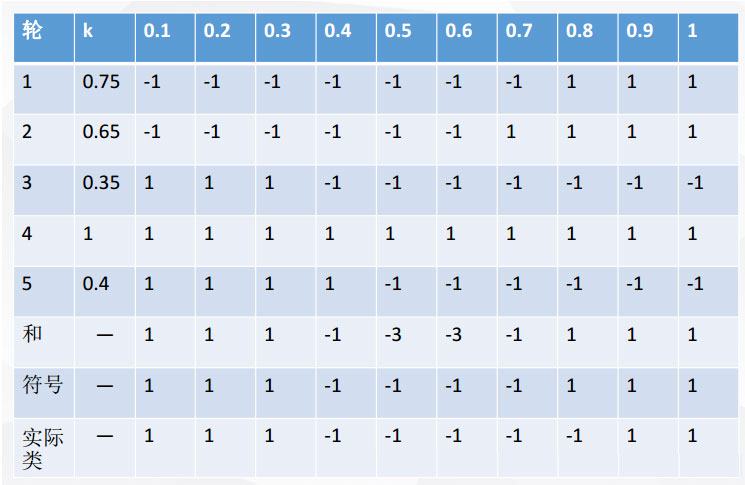
即是说当我们模型拿捏不住样本属于哪个,或者是分裂时的阈值,我们多做几次,得到多个结果,然后投票决定
优缺点:
(1) bagging通过降低基分类器的方差,改善了泛化误差;
(2)其性能依赖于基分类器的稳定性;如果基分类器不稳定,bagging有助于降低训练数据的随机波动导致的误差;如果稳定,则集成分类器的误差主要由基分类器的偏倚引起;
(3)由于每个样本被选中的概率相同,因此bagging并不侧重于训练数据集中的任何特定实例
1.优点,可以减小方差和减小过拟合
2.缺点,重复有放回采样的道德样本集改变了数据原有的分布,因此在一定程度上引入了偏差,对最终的结果预测会造成一定程度的影响
为什么说bagging算法会减少方差?
首先我们来看看偏差和方差的概念
偏差:描述的是预测值(估计值)的期望与真实值之间的差距。偏差越大,越偏离真实数据
方差:描述的是预测值的变化范围,离散程度,也就是离其期望值的距离。方差越大
- bias描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low bias,就得复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting),过拟合对应上图是high variance,点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
- varience描述的是样本上训练出来的模型在测试集上的表现,要想在variance上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应上图是high bias,点偏离中心。low variance对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准。
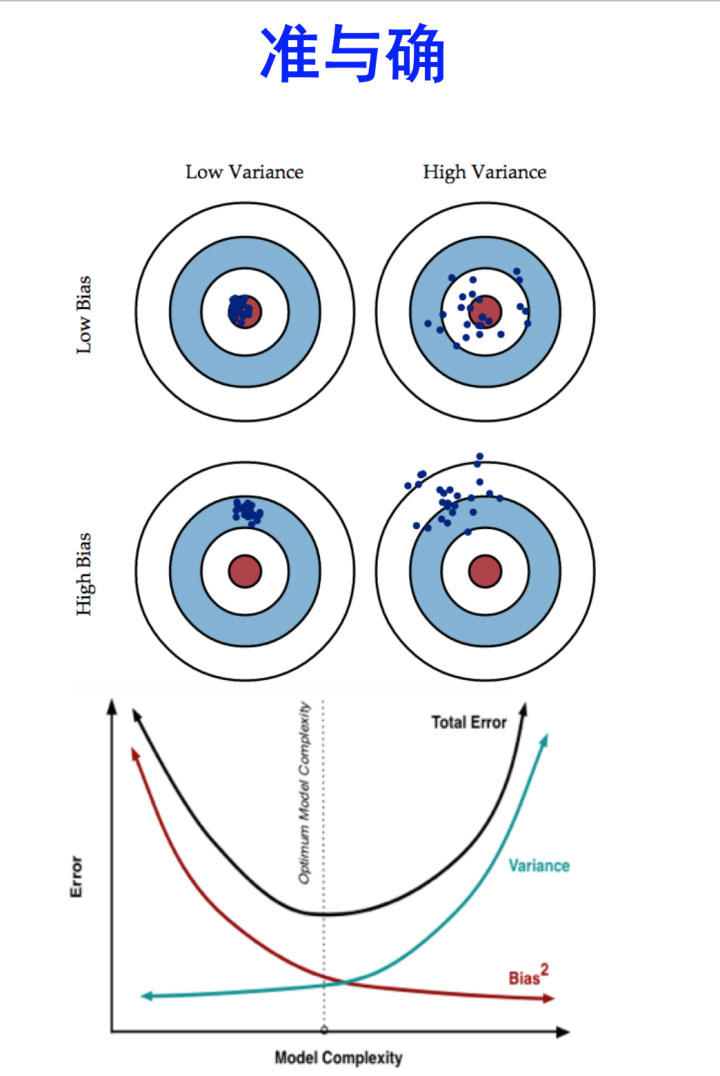
bagging是对许多强(甚至过强)的分类器求平均。在这里,每个单独的分类器的bias都是低的,平均之后bias依然低;而每个单独的分类器都强到可能产生overfitting的程度,也就是variance高,求平均的操作起到的作用就是降低这个variance。
boosting是把许多弱的分类器组合成一个强的分类器。弱的分类器bias高,而强的分类器bias低,所以说boosting起到了降低bias的作用。variance不是boosting的主要考虑因素。boosting则是迭代算法,每一次迭代都根据上一次迭代的预测结果对样本进行加权,所以随着迭代不断进行,误差会越来越小,所以模型的bias会不断降低。这种算法无法并行,例子比如adaptive boosting
bagging和rand forest
1)rand forest是选与输入样本的数目相同多的次数(可能一个样本会被选取多次,同时也会造成一些样本不会被选取到),而bagging一般选取比输入样本的数目少的样本
2)bagging是用全部特征来得到分类器,而rand forest是需要从全部特征中选取其中的一部分来训练得到分类器; 一般rand forest效果比bagging效果好!
三、bagging用于分类
我们使用葡萄酒数据集进行建模(数据处理):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
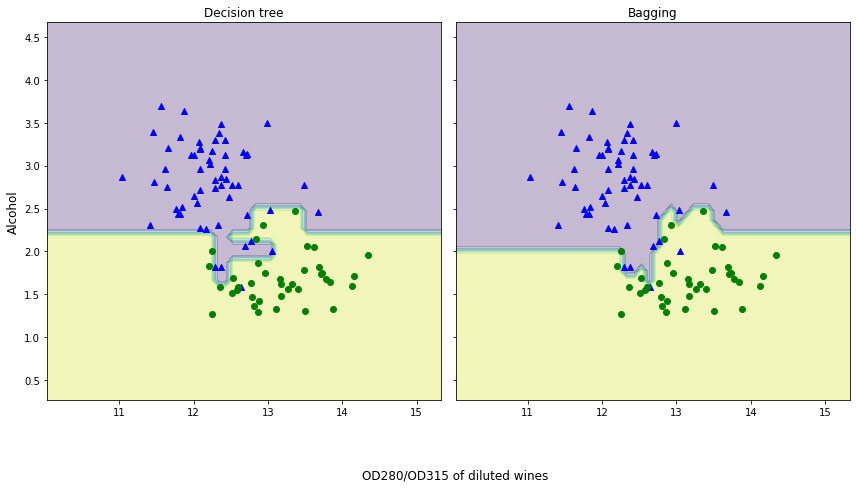
# -*- coding: utf-8 -*-"""created on tue aug 11 10:12:48 2020@author: admin"""## 我们使用葡萄酒数据集进行建模(数据处理)import pandas as pd df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=none)df_wine.columns = ['class label', 'alcohol','malic acid', 'ash','alcalinity of ash','magnesium', 'total phenols', 'flavanoids', 'nonflavanoid phenols','proanthocyanins','color intensity', 'hue','od280/od315 of diluted wines','proline']df_wine['class label'].value_counts()'''2 711 593 48name: class label, dtype: int64'''df_wine = df_wine[df_wine['class label'] != 1] # drop 1 classy = df_wine['class label'].valuesx = df_wine[['alcohol','od280/od315 of diluted wines']].valuesfrom sklearn.model_selection import train_test_split # 切分训练集与测试集from sklearn.preprocessing import labelencoder # 标签化分类变量le = labelencoder()y = le.fit_transform(y) #吧y值改为0和1 ,原来是2和3 x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2,random_state=1,stratify=y) #2、8分## 我们使用单一决策树分类:from sklearn.tree import decisiontreeclassifiertree = decisiontreeclassifier(criterion='entropy',random_state=1,max_depth=none) #选择决策树为基本分类器from sklearn.metrics import accuracy_score #计算准确率tree = tree.fit(x_train,y_train)y_train_pred = tree.predict(x_train)y_test_pred = tree.predict(x_test)tree_train = accuracy_score(y_train,y_train_pred) #训练集准确率tree_test = accuracy_score(y_test,y_test_pred) #测试集准确率print('decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))#decision tree train/test accuracies 1.000/0.833## 我们使用baggingclassifier分类:from sklearn.ensemble import baggingclassifiertree = decisiontreeclassifier(criterion='entropy',random_state=1,max_depth=none) #选择决策树为基本分类器bag = baggingclassifier(base_estimator=tree,n_estimators=500,max_samples=1.0,max_features=1.0,bootstrap=true, bootstrap_features=false,n_jobs=1,random_state=1)from sklearn.metrics import accuracy_scorebag = bag.fit(x_train,y_train)y_train_pred = bag.predict(x_train)y_test_pred = bag.predict(x_test)bag_train = accuracy_score(y_train,y_train_pred)bag_test = accuracy_score(y_test,y_test_pred)print('bagging train/test accuracies %.3f/%.3f' % (bag_train,bag_test))#bagging train/test accuracies 1.000/0.917'''我们可以对比两个准确率,测试准确率较之决策树得到了显著的提高我们来对比下这两个分类方法上的差异'''## 我们来对比下这两个分类方法上的差异x_min = x_train[:, 0].min() - 1x_max = x_train[:, 0].max() + 1y_min = x_train[:, 1].min() - 1y_max = x_train[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))for idx, clf, tt in zip([0, 1],[tree, bag],['decision tree', 'bagging']): clf.fit(x_train, y_train) z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) #ravel()方法将数组维度拉成一维数组,np.c_是按行连接两个矩阵,就是把两矩阵左右相加,要求行数相等 z = z.reshape(xx.shape) axarr[idx].contourf(xx, yy, z, alpha=0.3) axarr[idx].scatter(x_train[y_train==0, 0],x_train[y_train==0, 1],c='blue', marker='^') axarr[idx].scatter(x_train[y_train==1, 0],x_train[y_train==1, 1],c='green', marker='o') axarr[idx].set_title(tt)axarr[0].set_ylabel('alcohol', fontsize=12)plt.tight_layout()plt.text(0, -0.2,s='od280/od315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transaxes)plt.show()'''从结果图看起来,三个节点深度的决策树分段线性决策边界在bagging集成中看起来更加平滑''' |
|
1
|
class sklearn.ensemble.baggingclassifier(base_estimator=none, n_estimators=10, max_samples=1.0, max_features=1.0, bootstrap=true, bootstrap_features=false, oob_score=false, warm_start=false, n_jobs=none, random_state=none, verbose=0) |
参数说明:
- base_estimator:object or none。none代表默认是decisiontree,object可以指定基估计器(base estimator)
- n_estimators:int, optional (default=10) 。 要集成的基估计器的个数
- max_samples: int or float, optional (default=1.0)。决定从x_train抽取去训练基估计器的样本数量。int 代表抽取数量,float代表抽取比例
- max_features : int or float, optional (default=1.0)。决定从x_train抽取去训练基估计器的特征数量。int 代表抽取数量,float代表抽取比例
- bootstrap : boolean, optional (default=true) 决定样本子集的抽样方式(有放回和不放回)
- bootstrap_features : boolean, optional (default=false)决定特征子集的抽样方式(有放回和不放回)
- oob_score : bool 决定是否使用包外估计(out of bag estimate)泛化误差
- warm_start : bool, optional (default=false) 设置为true时,请重用上一个调用的解决方案以适合并为集合添加更多估计量,否则,仅适合一个全新的集合
- n_jobs : int, optional (default=none) fit和 并行运行的作业数predict。none除非joblib.parallel_backend上下文中,否则表示1 。-1表示使用所有处理器
- random_state : int, randomstate instance or none, optional (default=none)。如果int,random_state是随机数生成器使用的种子; 如果randomstate的实例,random_state是随机数生成器; 如果none,则随机数生成器是由np.random使用的randomstate实例
- verbose : int, optional (default=0)
属性介绍:
- estimators_ : list of estimators。the collection of fitted sub-estimators.
- estimators_samples_ : list of arrays
- estimators_features_ : list of arrays
- oob_score_ : float,使用包外估计这个训练数据集的得分。
- oob_prediction_ : array of shape = [n_samples]。在训练集上用out-of-bag估计计算的预测。 如果n_estimator很小,则可能在抽样过程中数据点不会被忽略。 在这种情况下,oob_prediction_可能包含nan。
四、bagging用于回归
再补充一下bagging用于回归
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
|
# -*- coding: utf-8 -*-"""created on tue aug 11 10:12:48 2020@author: admin"""# 从 sklearn.datasets 导入波士顿房价数据读取器。from sklearn.datasets import load_boston# 从读取房价数据存储在变量 boston 中。boston = load_boston()# 从sklearn.cross_validation 导入数据分割器。from sklearn.model_selection import train_test_splitx = boston.datay = boston.target# 随机采样 25% 的数据构建测试样本,其余作为训练样本。x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=33, test_size=0.25) # 从 sklearn.preprocessing 导入数据标准化模块。from sklearn.preprocessing import standardscaler# 分别初始化对特征和目标值的标准化器。ss_x = standardscaler()ss_y = standardscaler()# 分别对训练和测试数据的特征以及目标值进行标准化处理。x_train = ss_x.fit_transform(x_train)x_test = ss_x.transform(x_test)y_train = ss_y.fit_transform(y_train.reshape(-1,1))y_test = ss_y.transform(y_test.reshape(-1,1)) #baggingregressorfrom sklearn.ensemble import baggingregressorbagr = baggingregressor(n_estimators=500,max_samples=1.0,max_features=1.0,bootstrap=true, bootstrap_features=false,n_jobs=1,random_state=1)bagr.fit(x_train, y_train)bagr_y_predict = bagr.predict(x_test)from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error# 使用 r-squared、mse 以及 mae 指标对默认配置的随机回归森林在测试集上进行性能评估。print('r-squared value of baggingregressor:', bagr.score(x_test, y_test))print('the mean squared error of baggingregressor:', mean_squared_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(bagr_y_predict)))print('the mean absoluate error of baggingregressor:', mean_absolute_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(bagr_y_predict)))'''r-squared value of baggingregressor: 0.8417369323817341the mean squared error of baggingregressor: 12.27192314456692the mean absoluate error of baggingregressor: 2.2523244094488195'''#随机森林实现from sklearn.ensemble import randomforestregressorrfr = randomforestregressor(random_state=1)rfr.fit(x_train, y_train)rfr_y_predict = rfr.predict(x_test)# 使用 r-squared、mse 以及 mae 指标对默认配置的随机回归森林在测试集上进行性能评估。print('r-squared value of randomforestregressor:', rfr.score(x_test, y_test))print('the mean squared error of randomforestregressor:', mean_squared_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(rfr_y_predict)))print('the mean absoluate error of randomforestregressor:', mean_absolute_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(rfr_y_predict)))'''r-squared value of randomforestregressor: 0.8083674472512408the mean squared error of randomforestregressor: 14.859436220472439the mean absoluate error of randomforestregressor: 2.4732283464566924'''#用bagging集成随机森林bagr = baggingregressor(base_estimator=rfr,n_estimators=500,max_samples=1.0,max_features=1.0,bootstrap=true, bootstrap_features=false,n_jobs=1,random_state=1)bagr.fit(x_train, y_train)bagr_y_predict = bagr.predict(x_test)# 使用 r-squared、mse 以及 mae 指标对默认配置的随机回归森林在测试集上进行性能评估。print('r-squared value of baggingregressor:', bagr.score(x_test, y_test))print('the mean squared error of baggingregressor:', mean_squared_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(bagr_y_predict)))print('the mean absoluate error of baggingregressor:', mean_absolute_error( ss_y.inverse_transform(y_test), ss_y.inverse_transform(bagr_y_predict)))'''r-squared value of baggingregressor: 0.8226953069216255the mean squared error of baggingregressor: 13.748435433319694the mean absoluate error of baggingregressor: 2.3744811023622048''' |
以上就是详解bagging算法的原理及python实现的详细内容,更多关于python bagging算法 的资料请关注服务器之家其它相关文章!
原文链接:https://www.cnblogs.com/cgmcoding/p/13567288.html










