时间小波能量谱
- 反映信号的小波能量沿时间轴的分布。
由于小波变换具有等距效应,所以有:
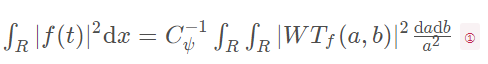
式中
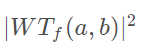
表示信号强度,对于式①在平移因子b方向上进行加权积分
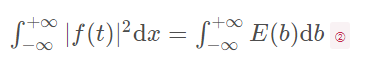
式中
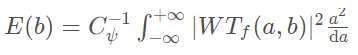
代表时间-小能量谱
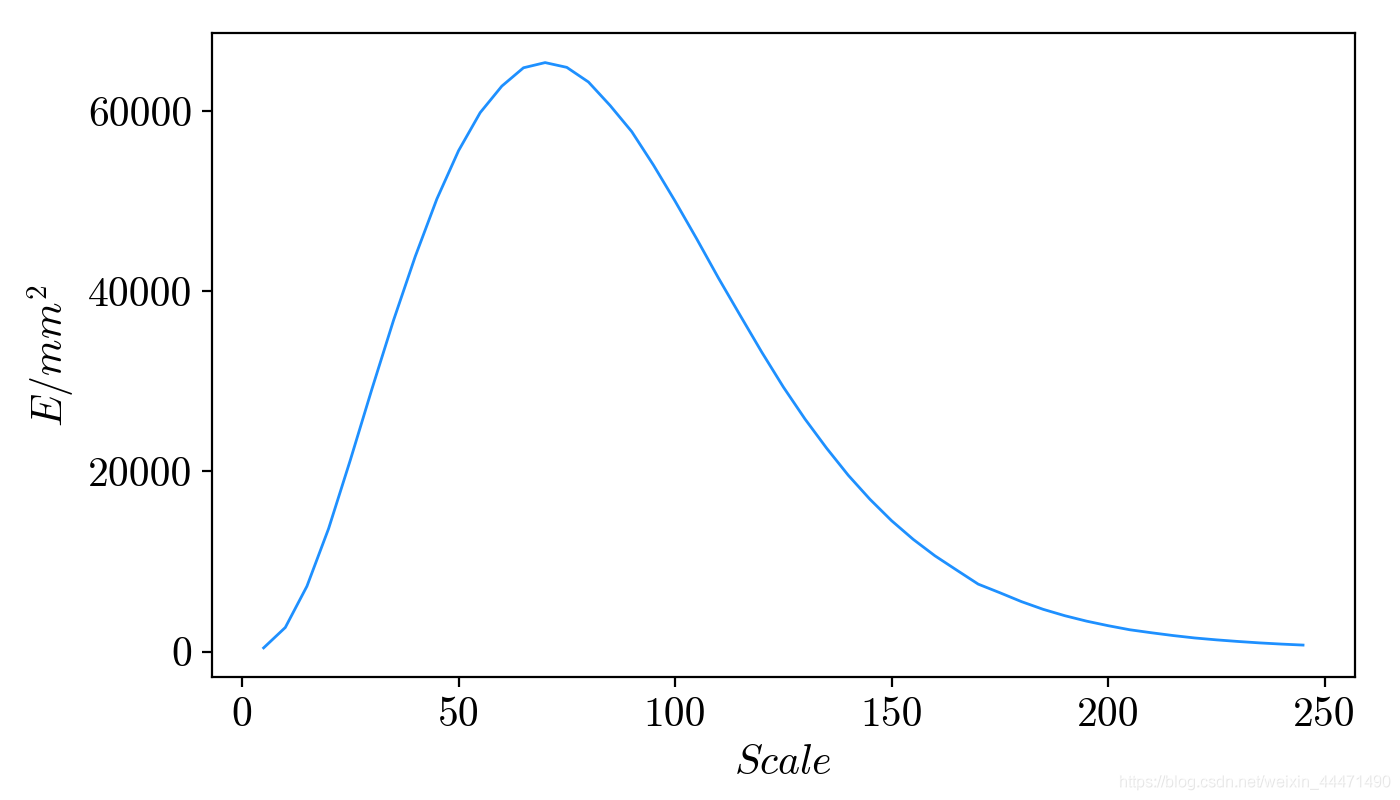
尺度小波能量谱
- 反映信号的小波能量随尺度的变化情况。
同理,对式①在尺度方向上进行加权积分:
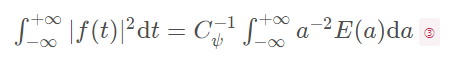
式中
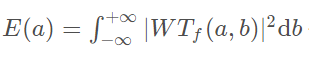
连续小波变换
- 连续小波变换的结果是一个小波系数矩阵,随着尺度因子和位移因子变化。然后将系数平方后得到小波能量,把每个尺度因子对应的所有小波能量进行叠加,那么就可以得到随尺度因子变换的小波能量谱曲线。把尺度换算成频率后,这条曲线就可视为是频谱图。
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
|
import pandas as pdimport numpy as npimport matplotlib.pyplot as pltimport pywtfrom mpl_toolkits.mplot3d import axes3dfrom matplotlib.ticker import multiplelocator, formatstrformatter# 解决负号显示问题plt.rcparams['axes.unicode_minus'] = false # 解决保存图像是负号'-'显示为方块的问题plt.rcparams.update({'text.usetex': false, 'font.family': 'serif', 'font.serif': 'cmr10', 'mathtext.fontset': 'cm'})font1 = {'family': 'simhei', 'weight': 'normal', 'size': 12}font2 = {'family': 'times new roman', 'weight': 'normal', 'size': 18}label = {'family': 'simhei', 'weight': 'normal', 'size': 15}xlsx_path = "../小波能量谱作图.xlsx"sheet_name = "表名" data_arr = pd.read_excel(xlsx_path, sheet_name=sheet_name)column_name = '列名' row = 1024y = data_arr[column_name][0:row]x = data_arr['time'][0:row]scale = np.arange(1, 50)wavelet = 'gaus1' # 'morl' 'gaus1' 小波基函数# 时间-尺度小波能量谱def time_scale_spectrum(): coefs, freqs = pywt.cwt(y, scale, wavelet) # np.arange(1, 31) 第一个参数必须 >=1 'morl' 'gaus1' scale_freqs = np.power(freqs, -1) # 对频率freqs 取倒数变为尺度 fig = plt.figure(figsize=(5, 4)) ax = axes3d(fig) # x:time y:scale z:amplitude x = np.arange(0, row, 1) # [0-1023] y = scale_freqs x, y = np.meshgrid(x, y) z = abs(coefs) # 绘制三维曲面图 ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow') # 设置三个坐标轴信息 ax.set_xlabel('$mileage/km$', color='b', fontsize=12) ax.set_ylabel('$scale$', color='g', fontsize=12) ax.set_zlabel('$amplitude/mm$', color='r', fontsize=12) plt.draw() plt.show()# 时间小波能量谱def time_spectrum(): coefs, freqs = pywt.cwt(y, scale, wavelet) coefs_pow = np.power(coefs, 2) # 对二维数组中的数平方 spectrum_value = [0] * row # len(freqs) # 将二维数组按照里程叠加每个里程上的所有scale值 for i in range(row): sum = 0 for j in range(len(freqs)): sum += coefs_pow[j][i] spectrum_value[i] = sum fig = plt.figure(figsize=(7, 2)) line_width = 1 line_color = 'dodgerblue' line_style = '-' t1 = fig.add_subplot(1, 1, 1) t1.plot(x, spectrum_value, label='模拟', linewidth=line_width, color=line_color, linestyle=line_style) # t1.legend(loc='upper right', prop=font1, frameon=true) # lower ,left # 坐标轴名称 t1.set_xlabel('$time$', fontsize=15, fontdict=font1) # fontdict设置子图字体 t1.set_ylabel('$e/mm^2$', fontsize=15, fontdict=font1) # 坐标刻度值字体大小 t1.tick_params(labelsize=15) print(spectrum_value[269]) plt.show()# 尺度小波能量谱def scale_spectrum(): coefs, freqs = pywt.cwt(y, scale, wavelet) coefs_pow = np.power(coefs, 2) # 对二维数组中的数平方 scale_freqs = np.power(freqs, -1) # 对频率freqs 取倒数变为尺度 spectrum_value = [0] * len(freqs) # len(freqs) # 将二维数组按照里程叠加每个里程上的所有scale值 for i in range(len(freqs)): sum = 0 for j in range(row): sum += coefs_pow[i][j] spectrum_value[i] = sum fig = plt.figure(figsize=(7, 4)) line_width = 1 line_color1 = 'dodgerblue' line_style1 = '-' t1 = fig.add_subplot(1, 1, 1) t1.plot(scale_freqs, spectrum_value, label=column_name, linewidth=line_width, color=line_color1, linestyle=line_style1) # t1.legend(loc='upper right', prop=font1, frameon=true) # lower ,left # 坐标轴名称 t1.set_xlabel('$scale$', fontsize=15, fontdict=font1) # fontdict设置子图字体 t1.set_ylabel('$e/mm^2$', fontsize=15, fontdict=font1) # 坐标刻度值字体大小 t1.tick_params(labelsize=15) plt.show()# 通过调用下面三个不同的函数选择绘制能量谱time_scale_spectrum()# time_spectrum()# scale_spectrum() |
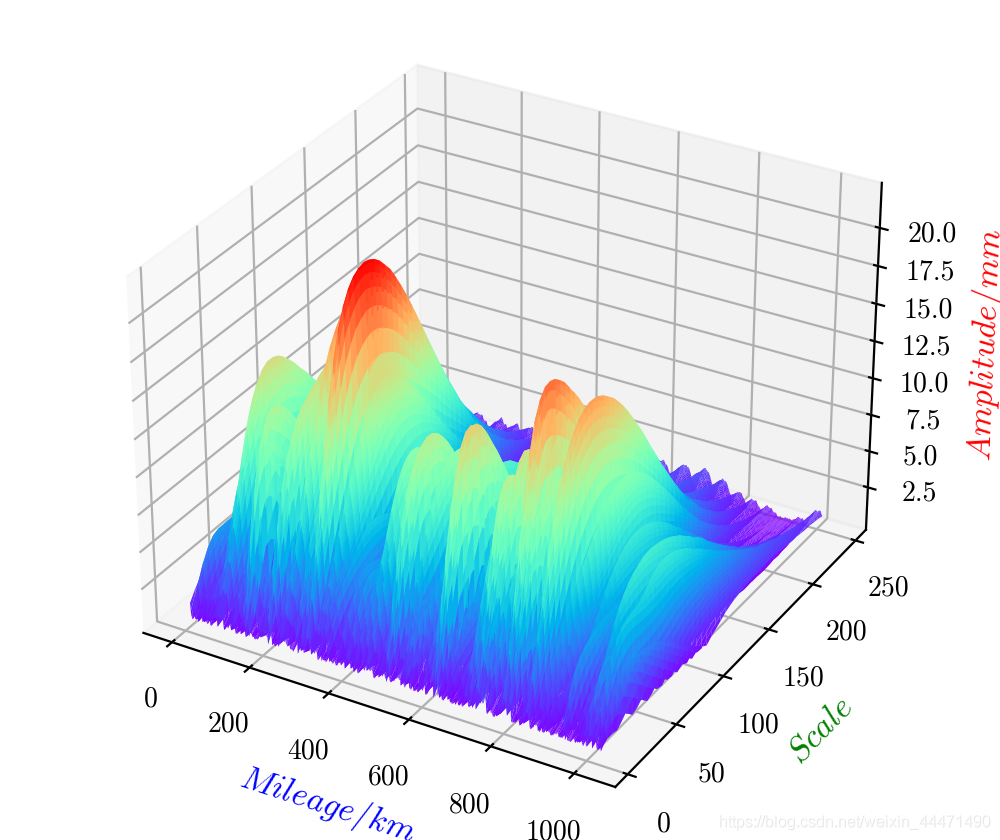
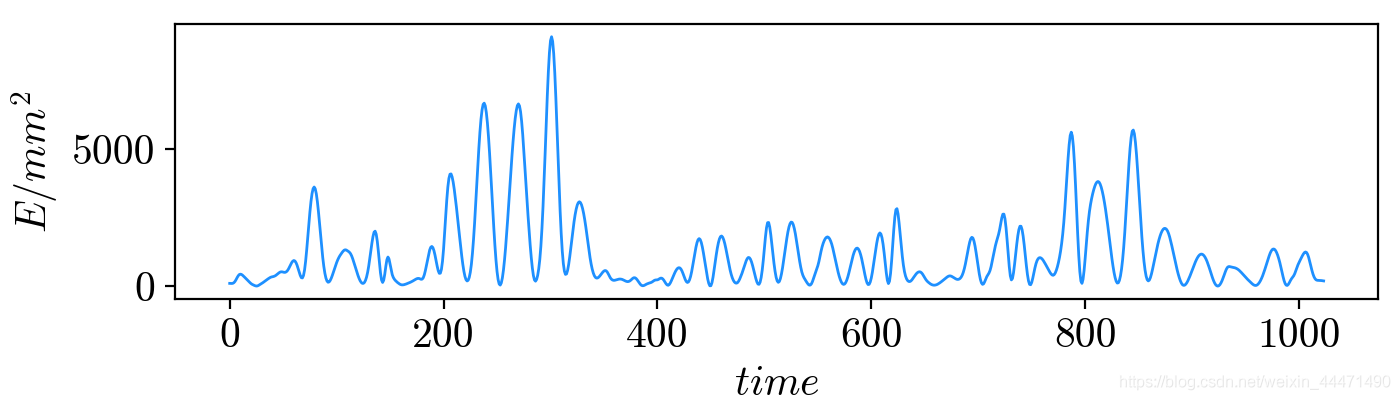
最终绘制的能量谱图如下:
1.时间-尺度小波能量谱
2.时间小波能量谱
3.尺度小波能量谱
到此这篇关于用python的绘图库(matplotlib)绘制小波能量谱的文章就介绍到这了,希望对你有帮助,更多相关用python绘制内容请搜索服务器之家以前的文章或继续浏览下面的相关文章,希望大家以后多多支持服务器之家!
原文链接:https://blog.csdn.net/weixin_44471490/article/details/115681322










