一、贝叶斯分类介绍
贝叶斯分类器是一个统计分类器。它们能够预测类别所属的概率,如:一个数据对象属于某个类别的概率。贝叶斯分类器是基于贝叶斯定理而构造出来的。对分类方法进行比较的有关研究结果表明:简单贝叶斯分类器(称为基本贝叶斯分类器)在分类性能上与决策树和神经网络都是可比的。在处理大规模数据库时,贝叶斯分类器已表现出较高的分类准确性和运算性能。基本贝叶斯分类器假设一个指定类别中各属性的取值是相互独立的。这一假设也被称为:类别条件独立,它可以帮助有效减少在构造贝叶斯分类器时所需要进行的计算。
二、贝叶斯定理
p(a|b) 条件概率 表示在b发生的前提下,a发生的概率;

基本贝叶斯分类器通常都假设各类别是相互独立的,即各属性的取值是相互独立的。对于特定的类别且其各属性相互独立,就会有:
p(ab|c) = p(a|c)*p(b|c)
三、贝叶斯分类案例
1.分类属性是离散
假设有样本数为6个的训练集数字如下:
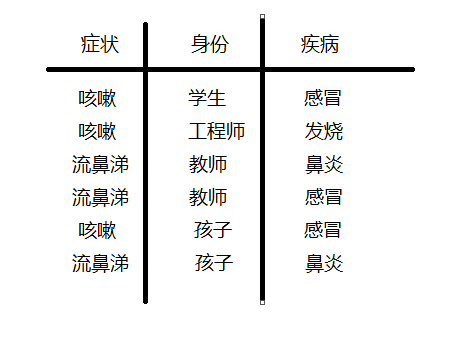
现在假设来又来了一个人是症状为咳嗽的教师,那这位教师是患上感冒、发烧、鼻炎的概率分别是多少呢?这个问题可以用贝叶斯分类来解决,最后三个疾病哪个概率高,就把这个咳嗽的教师划为哪个类,实质就是分别求p(感冒|咳嗽*教师)和p(发烧 | 咳嗽 * 教师)
p(鼻炎 | 咳嗽 * 教师) 的概率;
假设各个类别相互独立:

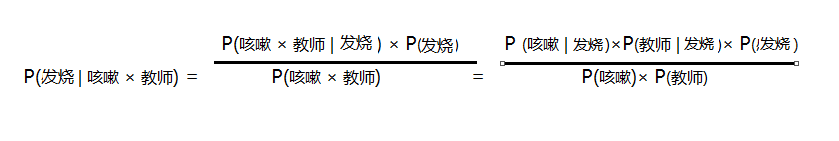

p(感冒)=3/6 p(发烧)=1/6 p(鼻炎)=2/6
p(咳嗽) = 3/6 p(教师)= 2/6
p(咳嗽 | 感冒) = 2/3 p(教师 | 感冒) = 1/3
故
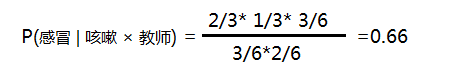
按以上方法可分别求 p(发烧 | 咳嗽 × 教师) 和p(鼻炎 |咳嗽 × 教师 )的概率;
2.分类属性连续
如果按上面的样本上加一个年龄的属性;因为年龄是连续,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算;这时,可以假设感冒、发烧、鼻炎分类的年龄都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数;
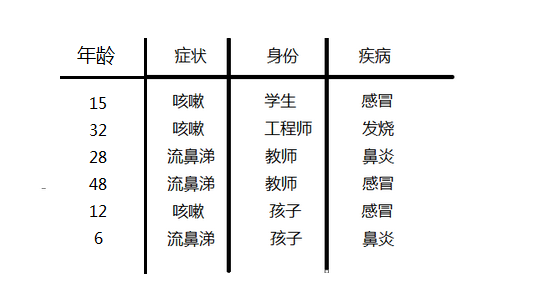
下面就以求p(年龄=15|感冒)下的概率为例说明:
第一:求在感冒类下的年龄平均值 u=(15+48+12)/3=25
第二:求在感冒类下年龄的方差 代入下面公司可求:方差=266
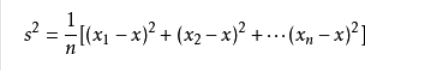
第三:把年龄=15 代入正太分布公式如下:参数代进去既可以求的p(age=15|感冒)的概率
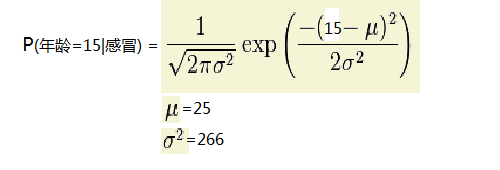
其他属性按离散方法可求;
四、概率值为0处理
假设有这种情况出现,在训练集上感冒的元祖有10个,有0个是孩子,有6个是学生,有4个教师;当分别求
p(孩子|感冒) =0; p(学生|感冒)=6/10 ; p(教师|感冒)=4/10 ;出现了概率为0的现象,为了避免这个现象,在假设训练元祖数量大量的前提下,可以使用拉普拉斯估计法,把每个类型加1这样可求的分别概率是
p(孩子|感冒) = 1/13 ; p(学生|感冒) = 7/13 ; p(教师|感冒)=4/13
五、垃圾邮件贝叶斯分类案例
1.准备训练集数据
假设postinglist为一个六个邮件内容,classvec=[0,1,0,1,0,1]为邮件类型,设1位垃圾邮件
|
1
2
3
4
5
6
7
8
9
|
def loaddataset(): postinglist =[['my','dog','has',' flea','problems','help','please'], ['mybe','not','take','him','to','dog','park','stupid'], ['my','dalmation','is','so','cute','i','love','hime'], ['stop','posting','stupid','worthless','garbage'], ['mr','licks','ate','my','steak','how','to','stop','hime'], ['quit','buying','worthless','dog','food','stupid','quit']] classvec =[0,1,0,1,0,1] return postinglist,classvec |
2.根据所有的邮件内容创建一个所有单词集合
|
1
2
3
4
5
|
def createvocablist(dataset): vocabset =set([]) for document in dataset: vocabset = vocabset | set(document) return list(vocabset) |
测试后获取所有不重复单词的集合见下一共:

3.根据2部所有不重复的单词集合对每个邮件内容向量化
|
1
2
3
4
5
|
def bagofwords2vecmn(vocablist,inputset): returnvec =[0]*len(vocablist) for word in inputset: returnvec[vocablist.index(word)] +=1 return returnvec |
测试后可得如下,打印内容为向量化的六个邮件内容
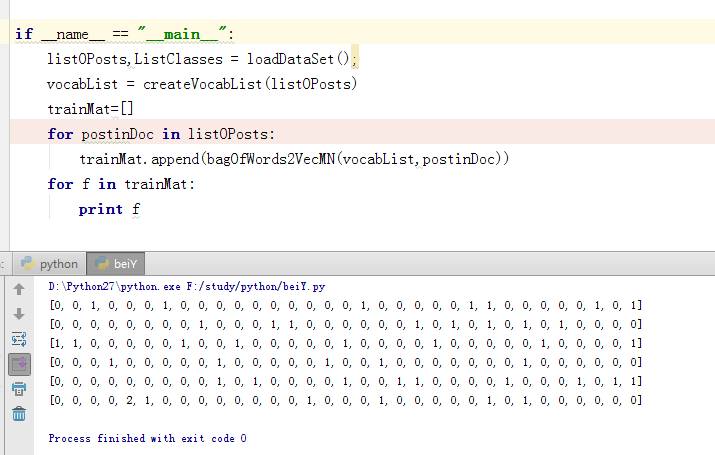
4.训练模型,此时就是分别求p(垃圾|文档) = p(垃圾)*p(文档|垃圾)/p(文档)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
def trainnbo(trainmatrix,traincategory): numtraindocs = len(trainmatrix) numwords =len(trainmatrix[0]) #计算p(垃圾)的概率 pabusive = sum(traincategory)/float(numtraindocs) #为了防止一个概率为0,假设都有一个 p0num =ones(numwords); p1num = ones(numwords) p0denom =2.0;p1denom=2.0; for i in range(numtraindocs): if traincategory[i] ==1: p1num +=trainmatrix[i] p1denom +=sum(trainmatrix[i]) else: p0num +=trainmatrix[i] p0denom +=sum(trainmatrix[i]) p1vect = np.log((p1num/p1denom)) p0vect = np.log(p0num/p0denom) return p0vect,p1vect,pabusive |
对训练模型进行测试结果如下:
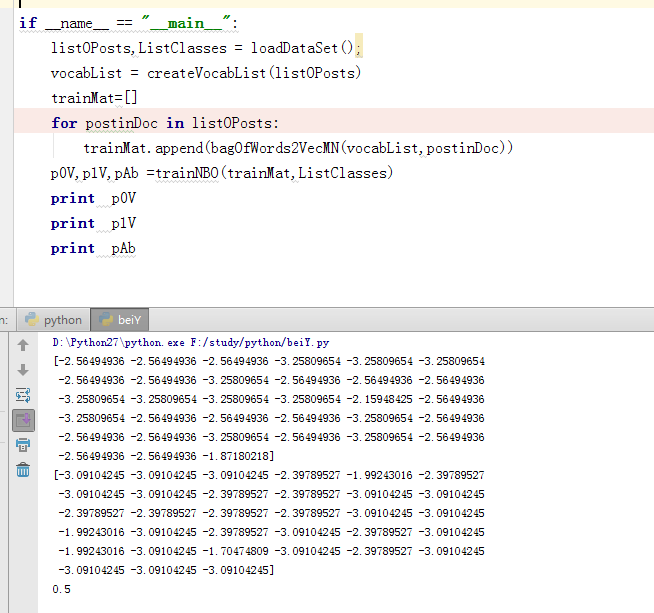
5.定义分类方法
|
1
2
3
4
5
6
7
|
def classifynb(vec2classify,p0vec,p1vec,pclass1): p1 =sum(vec2classify * p1vec) +math.log(pclass1) p0 = sum(vec2classify * p0vec)+math.log(1.0-pclass1) if p1>p0: return 1 else: return 0 |
6.以上分类完成,下面就对其进行测试,测试方法如下:
|
1
2
3
4
5
6
7
8
9
10
|
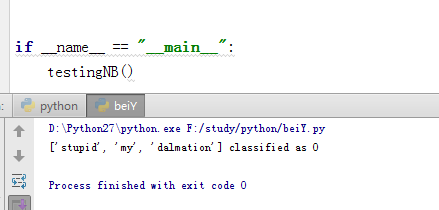
def testingnb(): listoposts,listclasses = loaddataset(); myvocablist = createvocablist(listoposts) trainmat=[] for postindoc in listoposts: trainmat.append(bagofwords2vecmn(myvocablist,postindoc)) p0v,p1v,pab =trainnbo(trainmat,listclasses) testentry =['stupid','my','dalmation'] thisdoc = array(bagofwords2vecmn(myvocablist,testentry)) print testentry,'classified as',classifynb(thisdoc,p0v,p1v,pab) |
结果如下:
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:https://blog.csdn.net/lisi1129/article/details/54927682










