今天整理之前写的代码,发现在做数模期间写的用python实现的遗传算法,感觉还是挺有意思的,就拿出来分享一下。
首先遗传算法是一种优化算法,通过模拟基因的优胜劣汰,进行计算(具体的算法思路什么的就不赘述了)。大致过程分为初始化编码、个体评价、选择,交叉,变异。
以目标式子 y = 10 * sin(5x) + 7 * cos(4x)为例,计算其最大值
首先是初始化,包括具体要计算的式子、种群数量、染色体长度、交配概率、变异概率等。并且要对基因序列进行初始化
|
1
2
3
4
5
6
7
8
9
10
|
pop_size = 500 # 种群数量 max_value = 10 # 基因中允许出现的最大值 chrom_length = 10 # 染色体长度 pc = 0.6 # 交配概率 pm = 0.01 # 变异概率 results = [[]] # 存储每一代的最优解,N个二元组 fit_value = [] # 个体适应度 fit_mean = [] # 平均适应度 pop = geneEncoding(pop_size, chrom_length) |
其中genEncodeing是自定义的一个简单随机生成序列的函数,具体实现如下
|
1
2
3
4
5
6
7
8
9
|
def geneEncoding(pop_size, chrom_length): pop = [[]] for i in range(pop_size): temp = [] for j in range(chrom_length): temp.append(random.randint(0, 1)) pop.append(temp) return pop[1:] |
编码完成之后就是要进行个体评价,个体评价主要是计算各个编码出来的list的值以及对应带入目标式子的值。其实编码出来的就是一堆2进制list。这些2进制list每个都代表了一个数。其值的计算方式为转换为10进制,然后除以2的序列长度次方减一,也就是全一list的十进制减一。根据这个规则就能计算出所有list的值和带入要计算式子中的值,代码如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
# 0.0 coding:utf-8 0.0 # 解码并计算值 import math def decodechrom(pop, chrom_length): temp = [] for i in range(len(pop)): t = 0 for j in range(chrom_length): t += pop[i][j] * (math.pow(2, j)) temp.append(t) return temp def calobjValue(pop, chrom_length, max_value): temp1 = [] obj_value = [] temp1 = decodechrom(pop, chrom_length) for i in range(len(temp1)): x = temp1[i] * max_value / (math.pow(2, chrom_length) - 1) obj_value.append(10 * math.sin(5 * x) + 7 * math.cos(4 * x)) return obj_value |
有了具体的值和对应的基因序列,然后进行一次淘汰,目的是淘汰掉一些不可能的坏值。这里由于是计算最大值,于是就淘汰负值就好了
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
# 0.0 coding:utf-8 0.0 # 淘汰(去除负值) def calfitValue(obj_value): fit_value = [] c_min = 0 for i in range(len(obj_value)): if(obj_value[i] + c_min > 0): temp = c_min + obj_value[i] else: temp = 0.0 fit_value.append(temp) return fit_value |
然后就是进行选择,这是整个遗传算法最核心的部分。选择实际上模拟生物遗传进化的优胜劣汰,让优秀的个体尽可能存活,让差的个体尽可能的淘汰。个体的好坏是取决于个体适应度。个体适应度越高,越容易被留下,个体适应度越低越容易被淘汰。具体的代码如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
# 0.0 coding:utf-8 0.0 # 选择 import random def sum(fit_value): total = 0 for i in range(len(fit_value)): total += fit_value[i] return total def cumsum(fit_value): for i in range(len(fit_value)-2, -1, -1): t = 0 j = 0 while(j <= i): t += fit_value[j] j += 1 fit_value[i] = t fit_value[len(fit_value)-1] = 1 def selection(pop, fit_value): newfit_value = [] # 适应度总和 total_fit = sum(fit_value) for i in range(len(fit_value)): newfit_value.append(fit_value[i] / total_fit) # 计算累计概率 cumsum(newfit_value) ms = [] pop_len = len(pop) for i in range(pop_len): ms.append(random.random()) ms.sort() fitin = 0 newin = 0 newpop = pop # 转轮盘选择法 while newin < pop_len: if(ms[newin] < newfit_value[fitin]): newpop[newin] = pop[fitin] newin = newin + 1 else: fitin = fitin + 1 pop = newpop |
以上代码主要进行了3个操作,首先是计算个体适应度总和,然后在计算各自的累积适应度。这两步都好理解,主要是第三步,转轮盘选择法。这一步首先是生成基因总数个0-1的小数,然后分别和各个基因的累积个体适应度进行比较。如果累积个体适应度大于随机数则进行保留,否则就淘汰。这一块的核心思想在于:一个基因的个体适应度越高,他所占据的累计适应度空隙就越大,也就是说他越容易被保留下来。
选择完后就是进行交配和变异,这个两个步骤很好理解。就是对基因序列进行改变,只不过改变的方式不一样
交配:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
# 0.0 coding:utf-8 0.0 # 交配 import random def crossover(pop, pc): pop_len = len(pop) for i in range(pop_len - 1): if(random.random() < pc): cpoint = random.randint(0,len(pop[0])) temp1 = [] temp2 = [] temp1.extend(pop[i][0:cpoint]) temp1.extend(pop[i+1][cpoint:len(pop[i])]) temp2.extend(pop[i+1][0:cpoint]) temp2.extend(pop[i][cpoint:len(pop[i])]) pop[i] = temp1 pop[i+1] = temp2 |
变异:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# 0.0 coding:utf-8 0.0 # 基因突变 import random def mutation(pop, pm): px = len(pop) py = len(pop[0]) for i in range(px): if(random.random() < pm): mpoint = random.randint(0, py-1) if(pop[i][mpoint] == 1): pop[i][mpoint] = 0 else: pop[i][mpoint] = 1 |
整个遗传算法的实现完成了,总的调用入口代码如下
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
# 0.0 coding:utf-8 0.0 import matplotlib.pyplot as plt import math from calobjValue import calobjValue from calfitValue import calfitValue from selection import selection from crossover import crossover from mutation import mutation from best import best from geneEncoding import geneEncoding print 'y = 10 * math.sin(5 * x) + 7 * math.cos(4 * x)' # 计算2进制序列代表的数值 def b2d(b, max_value, chrom_length): t = 0 for j in range(len(b)): t += b[j] * (math.pow(2, j)) t = t * max_value / (math.pow(2, chrom_length) - 1) return t pop_size = 500 # 种群数量 max_value = 10 # 基因中允许出现的最大值 chrom_length = 10 # 染色体长度 pc = 0.6 # 交配概率 pm = 0.01 # 变异概率 results = [[]] # 存储每一代的最优解,N个二元组 fit_value = [] # 个体适应度 fit_mean = [] # 平均适应度 # pop = [[0, 1, 0, 1, 0, 1, 0, 1, 0, 1] for i in range(pop_size)] pop = geneEncoding(pop_size, chrom_length) for i in range(pop_size): obj_value = calobjValue(pop, chrom_length, max_value) # 个体评价 fit_value = calfitValue(obj_value) # 淘汰 best_individual, best_fit = best(pop, fit_value) # 第一个存储最优的解, 第二个存储最优基因 results.append([best_fit, b2d(best_individual, max_value, chrom_length)]) selection(pop, fit_value) # 新种群复制 crossover(pop, pc) # 交配 mutation(pop, pm) # 变异 results = results[1:] results.sort() X = [] Y = [] for i in range(500): X.append(i) t = results[i][0] Y.append(t) plt.plot(X, Y) plt.show() |
最后调用了一下matplotlib包,把500代最优解的变化趋势表现出来。
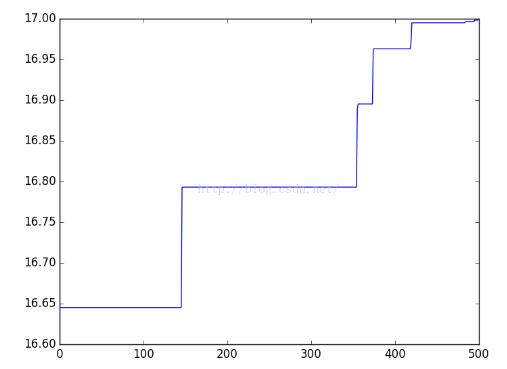
完整代码可以在github 查看
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://blog.csdn.net/czrzchao/article/details/52314455










