前段时间看了一期《最强大脑》,里面各种繁花曲线组合成了非常美丽的图形,一时心血来潮,想尝试自己用代码绘制繁花曲线,想怎么组合就怎么组合。
真实的繁花曲线使用一种称为繁花曲线规的小玩意绘制,繁花曲线规由相互契合大小两个圆组成,用笔插在小圆上的一个孔中,紧贴大圆的内壁滚动,就可以绘制出漂亮的图案。这个过程可以做一个抽象:有两个半径不相等的圆,大圆位置固定,小圆在大圆内部,小圆紧贴着大圆内壁滚动,求小圆上的某一点走过的轨迹。
进一步分析,小圆的运动可以分解为两个部分:小圆圆心绕大圆圆心公转、小圆绕自身圆心自转。设大圆圆心为a,半径为ra,小圆圆心为b,半径为rb,轨迹点为c,半径为rc(bc距离),设小圆公转的弧度为θ [0,∞),如图:
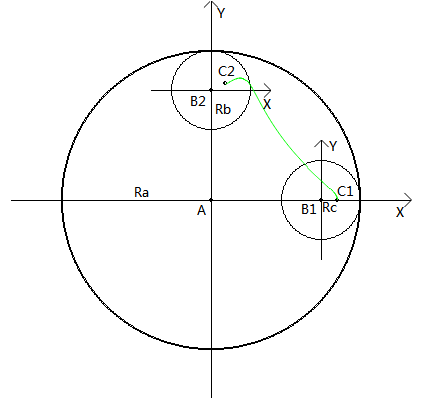
因为大圆的圆心坐标是固定的,要求得小圆上的某点的轨迹,需要先求出小圆当前时刻的圆心坐标,再求出小圆自转的弧度,最后求出小圆上某点的坐标。
第一步:求小圆圆心坐标
小圆圆心的公转轨迹是一个半径为 ra- rb 的圆,求小圆圆心坐标,相当于是求半径为 ra- rb 的圆上θ 弧度对应的点的坐标。
圆上的点的坐标公式为:
x = r * cos(θ), y = r * sin(θ)
小圆圆心坐标为:( xa+ (ra - rb) * cos(θ), ya + (ra - rb) * sin(θ) )
第二步:求小圆自转弧度
设小圆自转弧度为α,小圆紧贴大圆运动,两者走过的路程相同,因此有:
ra *θ = rb *α
小圆自转弧度α = (ra / rb) *θ
第三步:求点c坐标
点c相对小圆圆心b的公转轨迹是一个半径为 rc 的圆,类似第一步,有:
轨迹点c的坐标为:( xa+ rc* cos(θ), ya+ rc* sin(θ))
按照以上算法分析,用python代码实现如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
# -*- coding: utf-8 -*-import math'''功能: 已知圆的圆心和半径,获取某弧度对应的圆上点的坐标入参: center:圆心 radius:半径 radian:弧度'''def get_point_in_circle(center, radius, radian): return (center[0] + radius * math.cos(radian), center[1] - radius * math.sin(radian))'''功能: 内外圆a和b,内圆a沿着外圆b的内圈滚动,已知外圆圆心、半径,已知内圆半径,已知公转弧度和绕点半径,计算绕点坐标入参: center_a:外圆圆心 radius_a:外圆半径 radius_b:内圆半径 radius_c:绕点半径 radian:公转弧度'''def get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, radian): # 计算内圆圆心坐标 center_b = get_point_in_circle(center_a, radius_a - radius_b, radian) # 计算绕点弧度(公转为逆时针,则自转为顺时针) radian_c = 2.0*math.pi - ((radius_a / radius_b * radian) % (2.0*math.pi)) # 计算绕点坐标 return get_point_in_circle(center_b, radius_c, radian_c) |
有两点需要注意:
(1)屏幕坐标系左上角为原点,垂直向下为y正轴,与数学坐标系y轴方向相反,所以第14行y坐标为减法;
(2)默认公转为逆时针,则自转为顺时针,所以第30行求自转弧度时,使用了2π - α%(2π);
坐标已经计算出来,接下来使用pygame绘制。思想是以0.01弧度为一个步长,不断计算出新的坐标,把一系列坐标连起来就会形成轨迹图。
为了能够形成一个封闭图形,还需要知道绘制点什么时候会重新回到起点。想了一个办法,以x轴正半轴为基准线,每次绘制点到达基准线,计算此时绘制点与起点的距离,达到一定精度认为已经回到起点,形成封闭图形。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
''' 计算两点距离(平方和) '''def get_instance(p1, p2): return (p1[0] - p2[0]) * (p1[0] - p2[0]) + (p1[1] - p2[1]) * (p1[1] - p2[1]) '''功能: 获取绕点路径的所有点的坐标入参: center:外圆圆心 radius_a:外圆半径 radius_b:内圆半径 radius_c:绕点半径 shift_radian:每次偏移的弧度,默认0.01,值越小,精度越高,计算量越大'''def get_points(center, radius_a, radius_b, radius_c, shift_radian=0.01): # 转为实数 radius_a *= 1.0 radius_b *= 1.0 radius_c *= 1.0 p2 = 2*math.pi # 一圈的弧度为 2pi r_per_round = int(p2/shift_radian/4) + 1 # 一圈需要走多少步(弧度偏移多少次) # 第一圈的起点坐标 start_point = get_point_in_child_circle(center, radius_a, radius_b, radius_c, 0) points = [start_point] # 第一圈的路径坐标 for r in range(1, r_per_round): points.append(get_point_in_child_circle(center, radius_a, radius_b, radius_c, shift_radian*r)) # 以圈为单位,每圈的起始弧度为 2pi*round,某圈的起点坐标与第一圈的起点坐标距离在一定范围内,认为路径结束 for round in range(1, 100): s_radian = round*p2 s_point = get_point_in_child_circle(center, radius_a, radius_b, radius_c, s_radian) if get_instance(s_point, start_point) < 0.1: break points.append(s_point) for r in range(1, r_per_round): points.append(get_point_in_child_circle(center, radius_a, radius_b, radius_c, s_radian + shift_radian*r)) return points |
再加上绘制代码,完整代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
|
# -*- coding: utf-8 -*-import mathimport random'''功能: 已知圆的圆心和半径,获取某弧度对应的圆上点的坐标入参: center:圆心 radius:半径 radian:弧度'''def get_point_in_circle(center, radius, radian): return (center[0] + radius * math.cos(radian), center[1] - radius * math.sin(radian))'''功能: 内外圆a和b,内圆a沿着外圆b的内圈滚动,已知外圆圆心、半径,已知内圆半径、公转弧度,已知绕点半径,计算绕点坐标入参: center_a:外圆圆心 radius_a:外圆半径 radius_b:内圆半径 radius_c:绕点半径 radian:公转弧度'''def get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, radian): # 计算内圆圆心坐标 center_b = get_point_in_circle(center_a, radius_a - radius_b, radian) # 计算绕点弧度(公转为逆时针,则自转为顺时针) radian_c = 2.0*math.pi - ((radius_a / radius_b * radian) % (2.0*math.pi)) # 计算绕点坐标 center_c = get_point_in_circle(center_b, radius_c, radian_c) center_b_int = (int(center_b[0]), int(center_b[1])) return center_b_int, center_c''' 计算两点距离(平方和) '''def get_instance(p1, p2): return (p1[0] - p2[0]) * (p1[0] - p2[0]) + (p1[1] - p2[1]) * (p1[1] - p2[1]) '''功能: 获取绕点路径的所有点的坐标入参: center:外圆圆心 radius_a:外圆半径 radius_b:内圆半径 radius_c:绕点半径 shift_radian:每次偏移的弧度,默认0.01,值越小,精度越高,计算量越大'''def get_points(center_a, radius_a, radius_b, radius_c, shift_radian=0.01): # 转为实数 radius_a *= 1.0 radius_b *= 1.0 radius_c *= 1.0 p2 = 2*math.pi # 一圈的弧度为 2pi r_per_round = int(p2/shift_radian) + 1 # 一圈需要走多少步(弧度偏移多少次) # 第一圈的起点坐标 start_center, start_point = get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, 0) points = [start_point] centers = [start_center] # 第一圈的路径坐标 for r in range(1, r_per_round): center, point = get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, shift_radian*r) points.append(point) centers.append(center) # 以圈为单位,每圈的起始弧度为 2pi*round,某圈的起点坐标与第一圈的起点坐标距离在一定范围内,认为路径结束 for round in range(1, 100): s_radian = round*p2 s_center, s_point = get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, s_radian) if get_instance(s_point, start_point) < 0.1: break points.append(s_point) centers.append(s_center) for r in range(1, r_per_round): center, point = get_point_in_child_circle(center_a, radius_a, radius_b, radius_c, s_radian + shift_radian*r) points.append(point) centers.append(center) print(len(points)/r_per_round) return centers, pointsimport pygamefrom pygame.locals import *pygame.init()screen = pygame.display.set_mode((600, 400))clock = pygame.time.clock()color_black = (0, 0, 0)color_white = (255, 255, 255)color_red = (255, 0, 0)color_yello = (255, 255, 0)center = (300, 200)radius_a = 150radius_b = 110radius_c = 50test_centers, test_points = get_points(center, radius_a, radius_b, radius_c)test_idx = 2draw_point_num_per_tti = 5while true: for event in pygame.event.get(): if event.type==pygame.quit: pygame.quit() exit(0) screen.fill(color_white) pygame.draw.circle(screen, color_black, center, int(radius_a), 2) if test_idx <= len(test_points): pygame.draw.aalines(screen, (0, 0, 255), false, test_points[:test_idx], 1) if test_idx < len(test_centers): pygame.draw.circle(screen, color_black, test_centers[test_idx], int(radius_b), 1) pygame.draw.aaline(screen, color_black, test_centers[test_idx], test_points[test_idx], 1) test_idx = min(test_idx + draw_point_num_per_tti, len(test_points)) clock.tick(50) pygame.display.flip() |
效果:

以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://www.cnblogs.com/rmthy/p/8371544.html










