穷举算法(Exhaustive Attack method)是最简单的一种算法,其依赖于计算机的强大计算能力来穷尽每一种可能性,从而达到求解问题的目的。穷举算法效率不高,但是适应于一些没有规律可循的场合。
穷举算法基本思想
穷举算法的基本思想就是从所有可能的情况中搜索正确的答案,其执行步骤如下:
(1)对于一种可能的情况,计算其结果。
(2)判断结果是否符合要求,如果不满足则执行第(1)步来搜索下一个可能的情况;如果符合要求,则表示寻找到一个正确答案。
在使用穷举法时,需要明确问题的答案的范围,这样才可以在指定的范围内搜索答案。指定范围之后,就可以使用循环语句和条件语句逐步验证候选答案的正确性,从而得到需要的正确答案。
穷举算法举例
鸡兔同笼问题最早记载于1500年前的《孙子兵法》,这是一个非常有名的问题。鸡兔同笼的原文如下:
今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几只?
这个问题的大致意思是:在一个笼子里关着若干只鸡和若干只兔,从上面数共有35个头,从下面数共有94只脚。问笼中鸡和兔的数量各是多少?
穷举算法
这个问题需要计算鸡的数量和兔的数量,我们通过分析可以知道鸡的数量应该在1~35之间。这样我们可以使用穷举法来逐个判断是否符合,从而搜索答案。
采用穷举法求解鸡兔同笼问题的程序示例代码如下:
/*
输入参数head是笼中头的总数,foot是笼中脚的总数,chicken是鸡的总数,rabbit是兔的总数
返回结果为0,表示没有搜索到符合条件的结果;
返回结果为1,表示搜索到了符合条件的结果
*/
int qiongju(int head,int foot,int *chicken,int * rabbit)
{
int re,i,j;
re=0;
for(i=0;i<=head,i++) //进行循环
{
j=head-i;
if(i*2+j*4==foot) //进行判断
{
re=1; //找到答案
*chicken=i;
*rabbit=j;
}
}
return re;
}
穷举算法求解鸡兔同笼问题
完整的琼剧算法求解鸡兔同笼问题的程序代码如下:
#include<iostream>
using namespace std;
/*
输入参数head是笼中头的总数,foot是笼中脚的总数,chicken是鸡的总数,rabbit是兔的总数
返回结果为0,表示没有搜索到符合条件的结果;
返回结果为1,表示搜索到了符合条件的结果
*/
int qiongju(int head,int foot,int *chicken,int * rabbit)
{
int re,i,j;
re=0;
for(i=0;i<=head;i++) //进行循环
{
j=head-i;
if(i*2+j*4==foot) //进行判断
{
re=1; //找到答案
*chicken=i;
*rabbit=j;
}
}
return re;
}
int main()
{
int chicken,rabbit,head,foot;
int re;
cout<<"穷举法求解鸡兔同笼问题:"<<endl;
cout<<"请输入头数:";
cin>>head;
cout<<"请输入脚数:";
cin>>foot;
re=qiongju(head,foot,&chicken,&rabbit);
if(re==1)
{
cout<<"鸡有"<<chicken<<"只,兔有"<<rabbit<<"只。"<<endl;
}
else
{
cout<<"无法求解!"<<endl;
}
return 0;
}
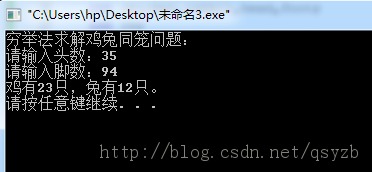
程序中,首先由用户输入头的总数和脚的总数,然后调用穷举法求解鸡兔同笼问题的函数,最后输出结果。
执行该程序,按照题目的要求输入数据,输出结果。