本文实例讲述了Python基于回溯法子集树模板解决数字组合问题。分享给大家供大家参考,具体如下:
问题
找出从自然数1、2、3、...、n中任取r个数的所有组合。
例如,n=5,r=3的所有组合为:
1,2,3
1,2,4
1,2,5
1,3,4
1,3,5
1,4,5
2,3,4
2,3,5
2,4,5
3,4,5
分析
换个角度,r=3的所有组合,相当于元素个数为3的所有子集。因此,在遍历子集树的时候,对元素个数不为3的子树剪枝即可。
注意,这里不妨使用固定长度的解。
直接套用子集树模板。
代码
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
'''数字组合问题'''n = 5r = 3a = [1,2,3,4,5] # 五个数字x = [0]*n # 一个解(n元0,1数组) 固定长度X = [] # 一组解def conflict(k): global n, r, x if sum(x[:k+1]) > r: # 部分解的长度超出r return True if sum(x[:k+1]) + (n-k-1) < r: # 部分解的长度加上剩下长度不够r return True return False # 无冲突# 套用子集树模板def comb(k): # 到达第k个元素 global n, x, X if k >= n: # 超出最尾的元素 #print(x) X.append(x[:]) # 保存(一个解) else: for i in [1, 0]: # 遍历元素 a[k] 的两种选择状态:1-选择,0-不选 x[k] = i if not conflict(k): # 剪枝 comb(k+1)# 根据一个解x,构造对应的一个组合def get_a_comb(x): global a return [y[0] for y in filter(lambda s:s[1]==1, zip(a, x))]# 根据一组解X,构造对应的一组组合def get_all_combs(X): return [get_a_comb(x) for x in X]# 测试comb(0)print(X)print(get_all_combs(X)) |
效果图
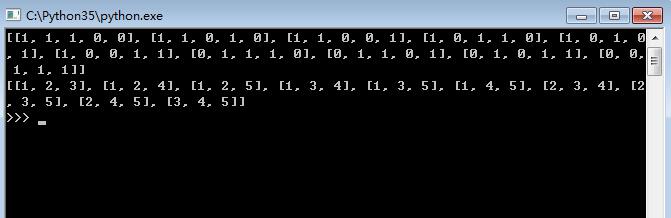
希望本文所述对大家Python程序设计有所帮助。
原文链接:http://www.cnblogs.com/hhh5460/p/6920382.html













