解决对接JAVA SM2加密遇到的坑_JAVA教程

解决对接JAVA SM2加密遇到的坑

2020-10-07 22:37qlee JAVA教程

这篇文章主要介绍了解决对接JAVA SM2加密遇到的坑，具有很好的参考价值，希望对大家有所帮助。一起跟随小编过来看看吧

遇到有接口需要使用国密的SM2算法，对方使用的是JAVA，我们使用的是go，原以为都是标准算法不会有什么大问题，结果巨坑无法..

对方使用的加密模块，SM2.java和SM2KeyPairs.java，不知道最初是谁开发的，网上貌似很多都是这个版本的实现，但是和go的交互总是有问题，用这个java模块加密的，go里面怎么也无法正确解密。仔细核对之后发现，这个java模块有几个地方并不符合GB/T32891的标准。

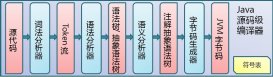
SM2加密的流程

SM2使用的椭圆曲线基点记为G，私钥为整数d, 公钥为P = dG.，这里K、G为椭圆曲线上的点，d为正整数

选择随机整数k，计算 C1 = kG, C4 = kP

以点C4的X/Y两坐标为参数，计算一组字节流T，与明文进行异或运算，结果为C2

已C1和明文组合，用SM3算法计算哈希值C3

将C1、C2、C3组合为加密后的密文

这里只要得到C4,便能进行解密，而C4 = kP = kdP = dkP = d(kC) = dC1。而C1是密文的一部分，所以有了私钥d便可以进行解密。

这里的P、G、C1、C4是椭圆曲线上的点，点的乘法只具有几何意义上，并非2X3=6的算术运算。

SM2 java模块与标准差异

1. 加密密文的组合

加密后的密文，标准为C1 || C3 || C2，C3位SM3哈系值，而这个库中结果为 C1 || C2 || C3。

2. Java BigInteger的最高位为1时编码错误

Java中，BigInteger的最高位为1时，toByteArray()得到的字节数组会多一位，在前面多了一个为0的字节，应该是要表示为正数。导致运算结果和其他语言的不一致。

3. 计算T时的差异

计算T时，需要用点C4的X坐标和Y坐标组合进行，这个库里直接调用bouncycastle库里，ECPoint类的getEncoded()的方法，得到的结果是在字节流里加了一个字节(0x4)，实际是不需要的，导致计算的字节流T有差异

4. 取点的X/Y坐标时没有正则化

java的bouncycastle库里，在椭圆曲线的计算中，使用了X/Y/Z三个坐标，而其他的实现可能是没有Z坐标的，所以调用点的坐标的时候，应该调用normalize()方法正则化后使用，这时Z坐标是1。

而在这个库中，并没有进行正则化的操作，导致加密结果无法与其他程序进行交互，除非对方也使用的bouncycastle库，可实现方式与其类似。

补充知识：SM2数字签名算法java实现

给出我的SM2数字签名算法代码Java实现，所属文件SM2Signer.java

				?

									@Override

									public BigInteger[] generateSignature(byte[] message) {

									  ECDomainParameters ec = key.getParameters();

									  BigInteger n = ec.getN(); //阶n

									  ECPoint G = ec.getG();  //基点G

									  BigInteger r, s;

									  // 获取私钥d

									  BigInteger d = ((ECPrivateKeyParameters)key).getD();

									  ECMultiplier basePointMultiplier = createBasePointMultiplier();

									  // 初始化随机数生成器

									  if (kCalculator.isDeterministic()) {

									    kCalculator.init(n, d, message);

									  } else {

									    kCalculator.init(n, random);

									  }

									  do { // 计算s

									    BigInteger k;

									    BigInteger e;

									    BigInteger tmp;

									    BigInteger tmp2;

									    do { // 计算r，参照GM/T 0003.2-2012 6.1

									      k = kCalculator.nextK();

									      ECPoint p = basePointMultiplier.multiply(G, k).normalize();

									      e = org.bouncycastle.util.BigIntegers.fromUnsignedByteArray(message);

									      // r = (e + x) mod n

									      r = p.getAffineXCoord().toBigInteger().add(e).mod(n);

									    } while (r.equals(ZERO) || r.add(k).equals(n));

									    // tmp = (1+d).inverse

									    tmp = d.add(ONE).modInverse(n);

									    // tmp2 = k - r*d

									    tmp2 = k.subtract(r.multiply(d));

									    s = tmp.multiply(tmp2).mod(n);

									  } while (s.equals(ZERO));

									  return new BigInteger[] {r,s};

									}