编辑距离
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的最少编辑操作次数。编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。一般来说,编辑距离越小,两个串的相似度越大。
例如将kitten一字转成sitting:('kitten' 和 ‘sitting' 的编辑距离为3)
sitten (k→s)
sittin (e→i)
sitting (→g)
Python中的Levenshtein包可以方便的计算编辑距离
包的安装: pip install python-Levenshtein
我们来使用下:
|
1
2
3
4
5
|
# -*- coding:utf-8 -*-import Levenshteintexta = '艾伦 图灵传'textb = '艾伦•图灵传'print Levenshtein.distance(texta,textb) |
上面的程序执行结果为3,但是只改了一个字符,为什么会发生这样的情况?
原因是Python将这两个字符串看成string类型,而在 string 类型中,默认的 utf-8 编码下,一个中文字符是用三个字节来表示的。
解决办法是将字符串转换成unicode格式,即可返回正确的结果1。
|
1
2
3
4
5
|
# -*- coding:utf-8 -*-import Levenshteintexta = u'艾伦 图灵传'textb = u'艾伦•图灵传'print Levenshtein.distance(texta,textb) |
接下来重点介绍下保重几个方法的作用:
|
1
|
Levenshtein.distance(str1, str2) |
计算编辑距离(也称Levenshtein距离)。是描述由一个字串转化成另一个字串最少的操作次数,在其中的操作包括插入、删除、替换。算法实现:动态规划。
|
1
|
Levenshtein.hamming(str1, str2) |
计算汉明距离。要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。
|
1
|
Levenshtein.ratio(str1, str2) |
计算莱文斯坦比。计算公式 r = (sum – ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和,ldist是类编辑距离。注意这里是类编辑距离,在类编辑距离中删除、插入依然+1,但是替换+2。
|
1
|
Levenshtein.jaro(s1, s2) |
计算jaro距离,Jaro Distance据说是用来判定健康记录上两个名字是否相同,也有说是是用于人口普查,我们先来看一下Jaro Distance的定义。
两个给定字符串S1和S2的Jaro Distance为:
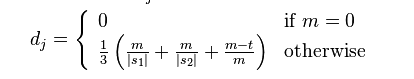
其中的m为s1, s2匹配的字符数,t是换位的数目。
两个分别来自S1和S2的字符如果相距不超过
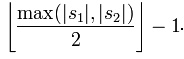
时,我们就认为这两个字符串是匹配的;而这些相互匹配的字符则决定了换位的数目t,简单来说就是不同顺序的匹配字符的数目的一半即为换位的数目t。举例来说,MARTHA与MARHTA的字符都是匹配的,但是这些匹配的字符中,T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符,t=2/2=1。
两个字符串的Jaro Distance即为:
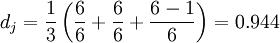
|
1
|
Levenshtein.jaro_winkler(s1, s2) |
计算Jaro–Winkler距离,而Jaro-Winkler则给予了起始部分就相同的字符串更高的分数,他定义了一个前缀p,给予两个字符串,如果前缀部分有长度为ι的部分相同,则Jaro-Winkler Distance为:
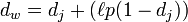
dj是两个字符串的Jaro Distance
ι是前缀的相同的长度,但是规定最大为4
p则是调整分数的常数,规定不能超过25,不然可能出现dw大于1的情况,Winkler将这个常数定义为0.1
这样,上面提及的MARTHA和MARHTA的Jaro-Winkler Distance为:
|
1
|
dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961 |
个人觉得算法可以完善的点:
去除停用词(主要是标点符号的影响)
针对中文进行分析,按照词比较是不是要比按照字比较效果更好?
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家学习或者使用python能有所帮助,如果有疑问大家可以留言交流。
其他参考资料:
https://en.wikipedia.org/wiki/Jaro%E2%80%93Winkler_distance
http://www.coli.uni-saarland.de/courses/LT1/2011/slides/Python-Levenshtein.html#Levenshtein-inverse










