通用形态学函数
上篇博文,我们介绍了形态学的基础腐蚀与膨胀操作,而将腐蚀与膨胀结合起来进行组合,我们就能实现开运算,闭运算等复杂的形态学运算。
在OpenCV中,它给我们提供的通用形态学函数为cv2.morphologyEx(),其完整定义如下:
def morphologyEx(src, op, kernel, dst=None, anchor=None, iterations=None, borderType=None, borderValue=None):
这些参数基本前面都介绍过,不过有一点需要说明,src原始图像必须是CV_8U,CV_16U,CV_16S,CV_32F,CV_64F中的一种。
当然,这里面还有一个陌生的参数就是op,它就是各种形态学的类别,具体类别如表所示:
| 类型 | 说明 | 意义 | 操作 |
|---|---|---|---|
| cv2.MORPH_ERODE | 腐蚀 | 腐蚀 | erode() |
| cv2.MORPH_DILATE | 膨胀 | 膨胀 | dilate() |
| cv2.MORPH_OPEN | 开运算 | 先腐蚀后膨胀 | dilate(erode()) |
| cv2.MORPH_CLOSE | 闭运算 | 先膨胀后腐蚀 | erode(dilate()) |
| cv2.MORPH_GRADIENT | 形态学梯度运算 | 膨胀图减腐蚀图 | dilate()-erode() |
| cv2.MORPH_TOPHAT | 顶帽运算 | 原始图像减开运算所得图像 | src-open() |
| cv2.MORPH_BLACKHAT | 黑帽运算 | 闭运算所得图像减原始图像 | close()-src |
| cv2.MORPH_HITMISS | 击中击不中 | 前景背景腐蚀运算的交集。仅仅支持CV8UC1二进制图像 | intersection(erode(src),erode(src1)) |
开运算
如上表所示,开运算是将原图像腐蚀,再对其进行膨胀操作。主要用于去噪,计数等。去噪我们已经通过上面的腐蚀操作就可以完成,下面我们来实现有趣的计数操作。
import cv2
import numpy as np
img = cv2.imread("open.jpg",cv2.IMREAD_UNCHANGED)
kernel = np.ones((9,9), np.float32)
result = cv2.morphologyEx(img,cv2.MORPH_OPEN,kernel,iterations=5)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,我们能将不同区域划分开来,效果如下:
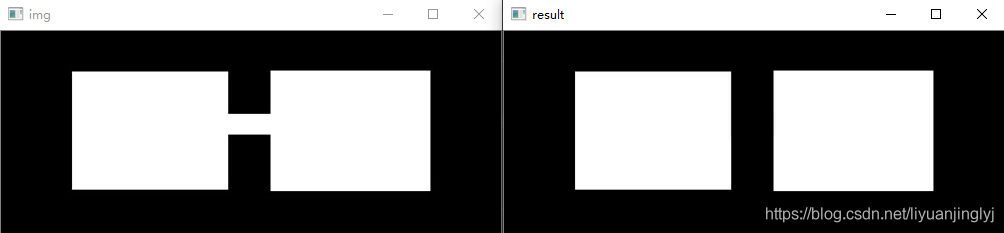
闭运算
闭运算是先膨胀后腐蚀的运算,它有助于关闭前景物体内部的小孔,或去除物体上的小黑点,还可以将不同的前景图像进行连接。下面,我们就将上图进行连接。
import cv2
import numpy as np
img = cv2.imread("close.jpg", cv2.IMREAD_UNCHANGED)
kernel = np.ones((10, 10), np.float32)
result = cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel, iterations=7)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,两个方块就连接为一个整体了,效果如下所示:
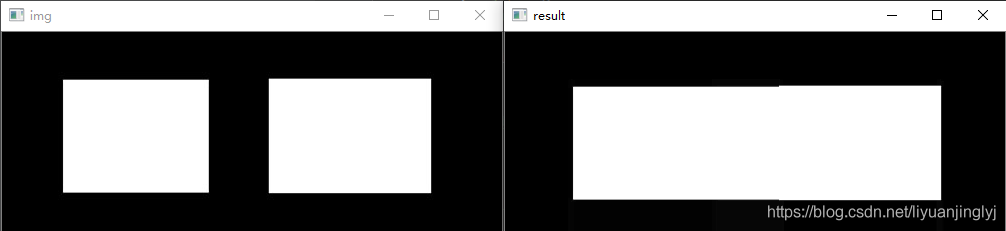
形态学梯度运算
形态学梯度运算是用图像膨胀后的图像减去腐蚀图像的运算,该操作可以获取原始图像中的前景图像的边缘。我们还是用上篇膨胀的图来测试,代码如下:
import cv2
import numpy as np
img = cv2.imread("8.jpg", cv2.IMREAD_UNCHANGED)
kernel = np.ones((5, 5), np.float32)
result = cv2.morphologyEx(img, cv2.MORPH_GRADIENT, kernel,iterations=2)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,我们的图像就中空了,效果如下:
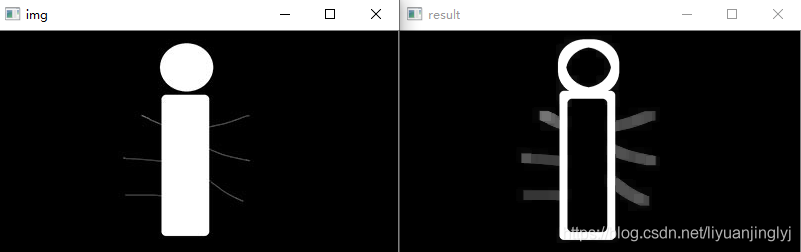
顶帽运算
顶帽运算是用原始图像减去其开运算图像的操作。它能够获取图像的噪声信息,或者得到比原图像的边缘更亮的边缘信息。也就是获取上图中的白色线条,具体代码如下:
import cv2
import numpy as np
img = cv2.imread("8.jpg", cv2.IMREAD_UNCHANGED)
kernel = np.ones((5, 5), np.float32)
result = cv2.morphologyEx(img, cv2.MORPH_TOPHAT, kernel,iterations=2)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,效果如下:
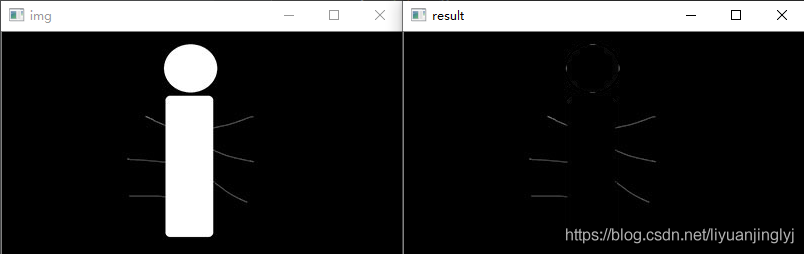
黑帽运算
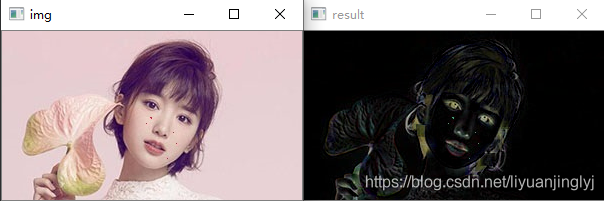
黑帽运算是用闭运算图像减去原始图像的操作。它能够获取内部的小孔,或前景色中的小黑点,亦或者得到比原始图像的边缘更暗的边缘部分。这里,我们用前面的人物图像,代码如下:
import cv2
import numpy as np
img = cv2.imread("4.jpg", cv2.IMREAD_UNCHANGED)
kernel = np.ones((5, 5), np.float32)
result = cv2.morphologyEx(img, cv2.MORPH_BLACKHAT, kernel,iterations=2)
cv2.imshow("img", img)
cv2.imshow("result", result)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,效果如下:
结构元函数
前面我们介绍过,结构元可以自定义,也可以通过cv2.getStructuringElement()函数生成。这里,我们来看看其完整的定义:
def getStructuringElement(shape, ksize, anchor=None):
shape:形状类型,取值如下表:
| 类型 | 意义 |
|---|---|
| cv2.MORPH_RECT | 矩形结构元,所有元素值为1 |
| cv2.MORPH_CROSS | 十字形结构元,对角线元素值为1 |
| cv2.MORPH_ELLIPSE | 椭圆形结构元素 |
ksize:结构元的大小
anchor:结构元的锚点位置,默认值(-1,1),是形状的中心。只有十字星型的形状与锚点位置紧密联系。在其他情况下,锚点位置仅用于形态学运算结果的调整。
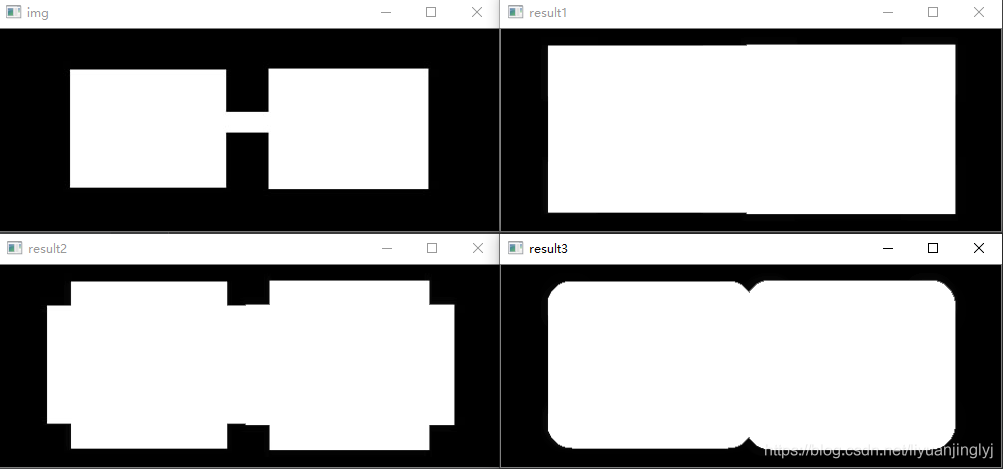
下面,我们将这三种形状类型都实现一遍,具体代码如下:
import cv2
img = cv2.imread("open.jpg", cv2.IMREAD_UNCHANGED)
kernel1 = cv2.getStructuringElement(cv2.MORPH_RECT,(50,50))
kernel2 = cv2.getStructuringElement(cv2.MORPH_CROSS,(50,50))
kernel3 = cv2.getStructuringElement(cv2.MORPH_ELLIPSE,(50,50))
result1 = cv2.dilate(img,kernel1)
result2 = cv2.dilate(img,kernel2)
result3 = cv2.dilate(img,kernel3)
cv2.imshow("img", img)
cv2.imshow("result1", result1)
cv2.imshow("result2", result2)
cv2.imshow("result3", result3)
cv2.waitKey()
cv2.destroyAllWindows()
运行之后,效果如下所示:
到此这篇关于OpenCV-Python实现通用形态学函数的文章就介绍到这了,更多相关OpenCV 通用形态学函数内容请搜索服务器之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持服务器之家!
原文链接:https://liyuanjinglyj.blog.csdn.net/article/details/113815570










