Python求解微分方程(数值解法)
对于一些微分方程来说,数值解法对于求解具有很好的帮助,因为难以求得其原方程。
比如方程:
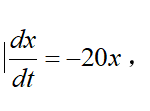
但是我们知道了它的初始条件,这对于我们叠代求解很有帮助,也是必须的。
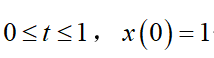
那么现在我们也用Python去解决这一些问题,一般的数值解法有欧拉法、隐式梯形法等,我们也来看看这些算法对叠代的精度有什么区别?
```python
```python
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
import os
#先从odeint函数直接求解微分方程
#创建欧拉法的类
class Euler:
#构造方法,当创建对象的时候,自动执行的函数
def __init__(self,h,y0):
#将对象与对象的属性绑在一起
self.h = h
self.y0 = y0
self.y = y0
self.n = 1/self.h
self.x = 0
self.list = [1]
#欧拉法用list列表,其x用y叠加储存
self.list2 = [1]
self.y1 = y0
#改进欧拉法用list2列表,其x用y1叠加储存
self.list3 = [1]
self.y2 = y0
#隐式梯形法用list3列表,其x用y2叠加储存
#欧拉法的算法,算法返回t,x
def countall(self):
for i in range(int(self.n)):
y_dere = -20*self.list[i]
#欧拉法叠加量y_dere = -20 * x
y_dere2 = -20*self.list2[i] + 0.5*400*self.h*self.list2[i]
#改进欧拉法叠加量 y_dere2 = -20*x(k) + 0.5*400*delta_t*x(k)
y_dere3 = (1-10*self.h)*self.list3[i]/(1+10*self.h)
#隐式梯形法计算 y_dere3 = (1-10*delta_t)*x(k)/(1+10*delta_t)
self.y += self.h*y_dere
self.y1 += self.h*y_dere2
self.y2 =y_dere3
self.list.append(float("%.10f" %self.y))
self.list2.append(float("%.10f"%self.y1))
self.list3.append(float("%.10f"%self.y2))
return np.linspace(0,1,int(self.n+1)), self.list,self.list2,self.list3
step = input("请输入你需要求解的步长:")
step = float(step)
work1 = Euler(step,1)
ax1,ay1,ay2,ay3 = work1.countall()
#画图工具plt
plt.figure(1)
plt.subplot(1,3,1)
plt.plot(ax1,ay1,"s-.",MarkerFaceColor = "g")
plt.xlabel("横坐标t",fontproperties = "simHei",fontsize =20)
plt.ylabel("纵坐标x",fontproperties = "simHei",fontsize =20)
plt.title("欧拉法求解微分线性方程步长为"+str(step),fontproperties = "simHei",fontsize =20)
plt.subplot(1,3,2)
plt.plot(ax1,ay2,"s-.",MarkerFaceColor = "r")
plt.xlabel("横坐标t",fontproperties = "simHei",fontsize =20)
plt.ylabel("纵坐标x",fontproperties = "simHei",fontsize =20)
plt.title("改进欧拉法求解微分线性方程步长为"+str(step),fontproperties = "simHei",fontsize =20)
plt.subplot(1,3,3)
plt.plot(ax1,ay3,"s-.",MarkerFaceColor = "b")
plt.xlabel("横坐标t",fontproperties = "simHei",fontsize =20)
plt.ylabel("纵坐标x",fontproperties = "simHei",fontsize =20)
plt.title("隐式梯形法求解微分线性方程步长为"+str(step),fontproperties = "simHei",fontsize =20)
plt.figure(2)
plt.plot(ax1,ay1,ax1,ay2,ax1,ay3,"s-.",MarkerSize = 3)
plt.xlabel("横坐标t",fontproperties = "simHei",fontsize =20)
plt.ylabel("纵坐标x",fontproperties = "simHei",fontsize =20)
plt.title("三合一图像步长为"+str(step),fontproperties = "simHei",fontsize =20)
ax = plt.gca()
ax.legend(("$Eular$","$fixed Eular$","$trapezoid$"),loc = "lower right",title = "legend")
plt.show()
os.system("pause")
对于欧拉法,它的叠代方法是:
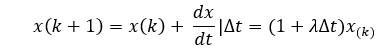
改进欧拉法的叠代方法:
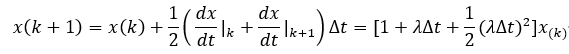
隐式梯形法:
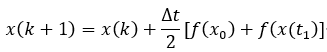
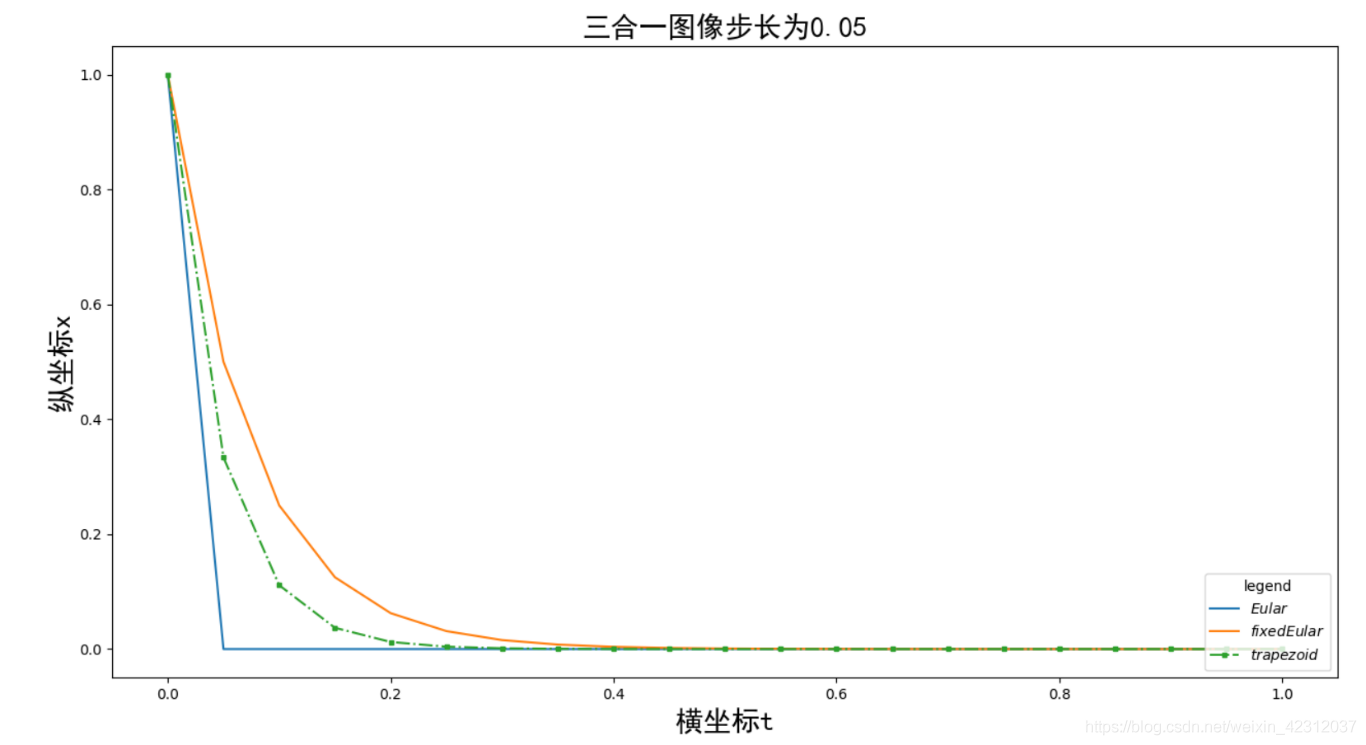
对于不同的步长,其求解的精度也会有很大的不同,我先放一几张结果图:
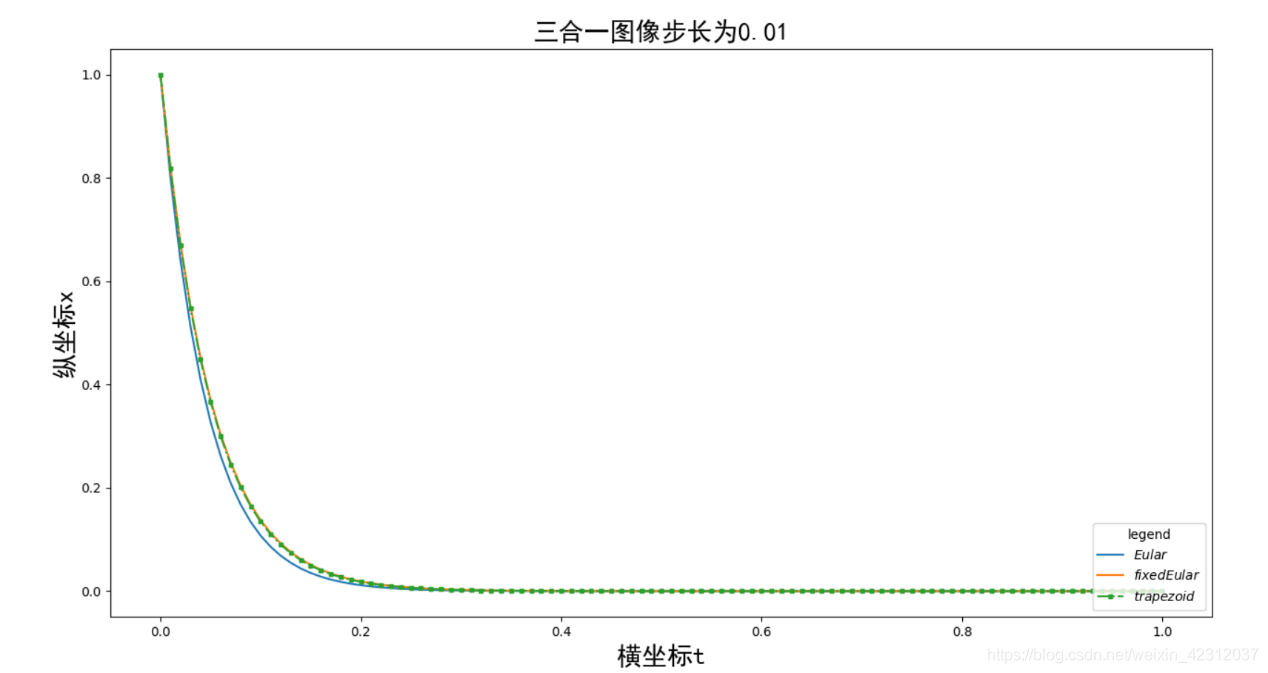
补充:基于python的微分方程数值解法求解电路模型
安装环境包
安装numpy(用于调节range) 和 matplotlib(用于绘图)
在命令行输入
pip install numpy pip install matplotlib
电路模型和微分方程
模型1
无损害,电容电压为5V,电容为0.01F,电感为0.01H的并联谐振电路
电路模型1
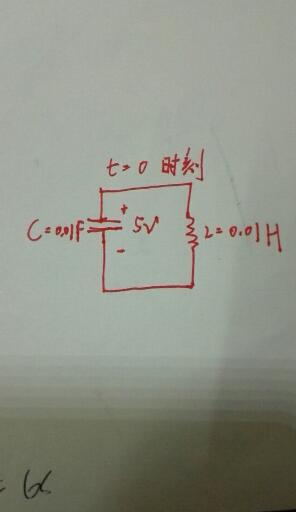
微分方程1
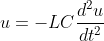
模型2
带电阻损耗的电容电压为5V,电容为0.01F,电感为0.01H的的并联谐振
电路模型2
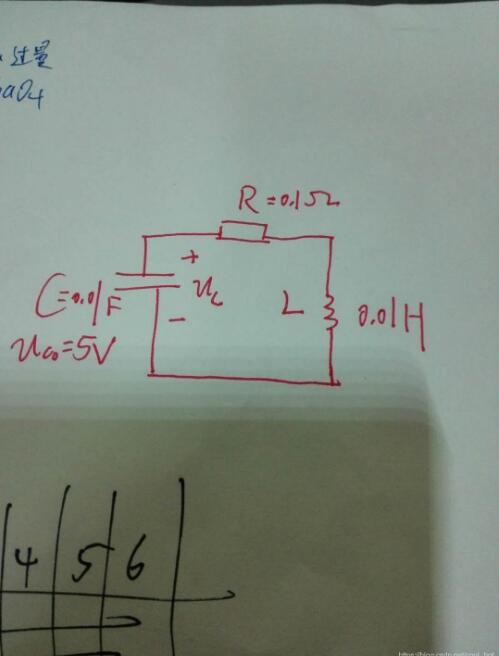
微分方程2
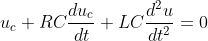
python代码
模型1
import numpy as np
import matplotlib.pyplot as plt
L = 0.01 #电容的值 F
C = 0.01 #电感的值 L
u_0 = 5 #电容的初始电压
u_dot_0 = 0
def equition(u,u_dot):#二阶方程
u_double_dot = -u/(L*C)
return u_double_dot
def draw_plot(time_step,time_scale):#时间步长和范围
u = u_0
u_dot = u_dot_0 #初始电压和电压的一阶导数
time_list = [0] #时间lis
Votage = [u] #电压list
plt.figure()
for time in np.arange(0,time_scale,time_step):#使用欧拉数值计算法 一阶近似
u_double_dot = equition(u,u_dot) #二阶导数
u_dot = u_dot + u_double_dot*time_step #一阶导数
u = u + u_dot*time_step #电压
time_list.append(time) #结果添加
Votage.append(u) #结果添加
print(u)
plt.plot(time_list,Votage,"b--",linewidth=1) #画图
plt.show()
plt.savefig("easyplot.png")
if __name__ == "__main__":
draw_plot(0.0001,1)
模型2
import numpy as np
import matplotlib.pyplot as plt
L = 0.01 #电容的值 F
C = 0.01 #电感的值 L
R = 0.1 #电阻值
u_0 = 5 #电容的初始电压
u_dot_0 = 0
def equition(u,u_dot):#二阶方程
u_double_dot =(-R*C*u_dot -u)/(L*C)
return u_double_dot
def draw_plot(time_step,time_scale):#时间步长和范围
u = u_0
u_dot = u_dot_0 #初始电压和电压的一阶导数
time_list = [0] #时间lis
Votage = [u] #电压list
plt.figure()
for time in np.arange(0,time_scale,time_step):#使用欧拉数值计算法 一阶近似
u_double_dot = equition(u,u_dot) #二阶导数
u_dot = u_dot + u_double_dot*time_step #一阶导数
u = u + u_dot*time_step #电压
time_list.append(time) #结果添加
Votage.append(u) #结果添加
print(u)
plt.plot(time_list,Votage,"b-",linewidth=1) #画图
plt.show()
plt.savefig("result.png")
if __name__ == "__main__":
draw_plot(0.0001,1)
数值解结果
模型1
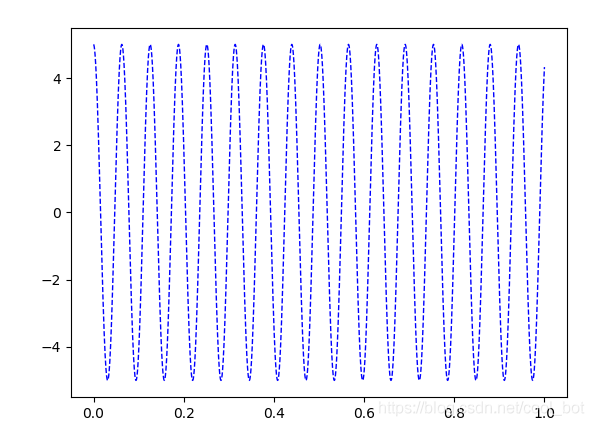
纵轴为电容两端电压,横轴为时间与公式计算一致
模型2结果
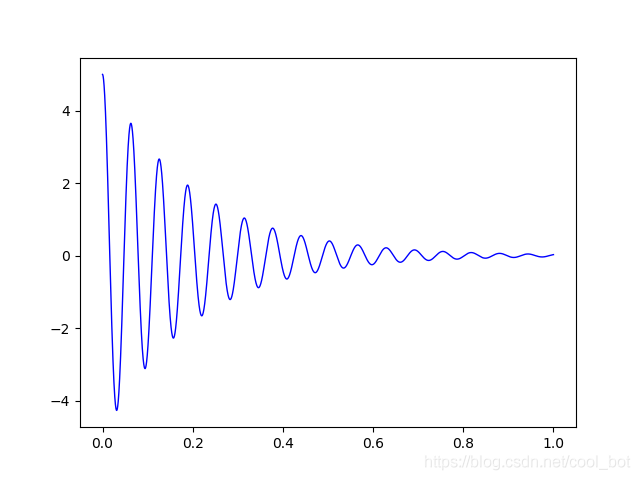
纵轴
为电容两端电压,横轴为时间标题
最后我们可以根据调节电阻到达不同的状态
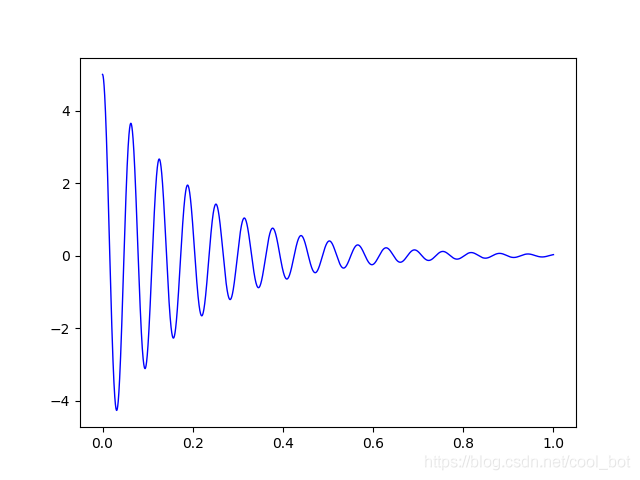
R=0.01,欠阻尼
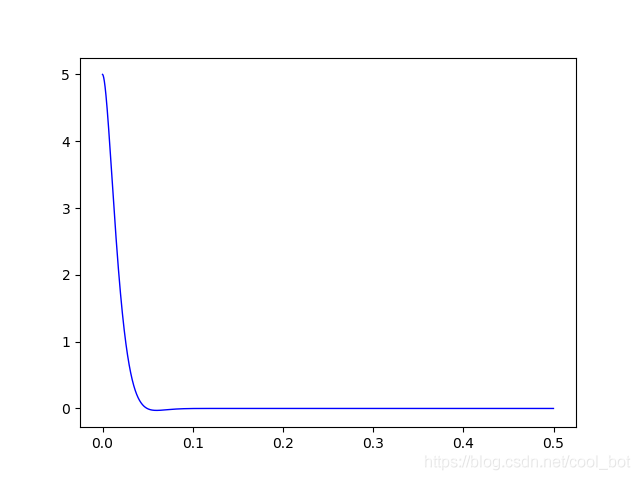
R=1.7,临界阻尼
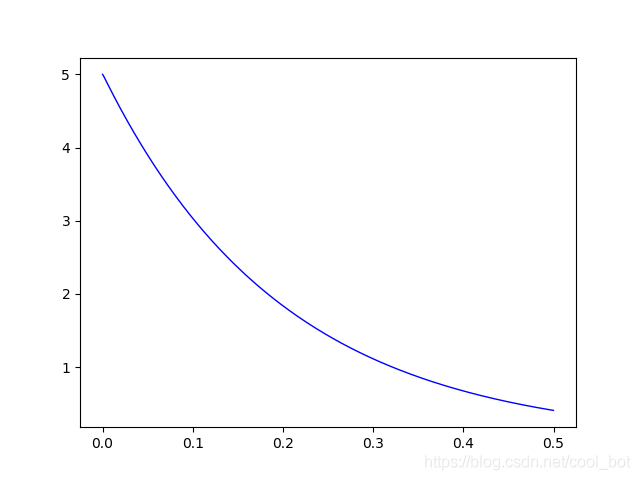
R=100,过阻尼
以上为个人经验,希望能给大家一个参考,也希望大家多多支持服务器之家。
原文链接:https://blog.csdn.net/weixin_42312037/article/details/111828651










