服务器之家：专注于服务器技术及软件下载分享
分类导航

PHP教程|ASP.NET教程|Java教程|ASP教程|编程技术|正则表达式|C/C++|IOS|C#|Swift|Android|VB|R语言|JavaScript|易语言|vb.net|

服务器之家 - 编程语言 - C# - C#数据结构之队列(Quene)实例详解

C#数据结构之队列(Quene)实例详解

2021-11-04 13:18Jimmy.Yang C#

这篇文章主要介绍了C#数据结构之队列(Quene),结合实例形式较为详细的讲述了队列的功能、原理与C#实现队列的相关技巧,需要的朋友可以参考下

本文实例讲述了C#数据结构之队列(Quene)。分享给大家供大家参考，具体如下：

队列(Quene)的特征就是“先进先出”，队列把所有操作限制在"只能在线性结构的两端"进行，更具体一点：添加元素必须在线性表尾部进行，而删除元素只能在线性表头部进行。

先抽象接口IQuene<T>

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
namespace 栈与队列
{
  public interface IQuene<T>
  {
    /// <summary>
    /// 取得队列实际元素的个数
    /// </summary>
    /// <returns></returns>
    public int Count();
    /// <summary>
    /// 判断队列是否为空
    /// </summary>
    /// <returns></returns>
    public bool IsEmpty();
    /// <summary>
    /// 清空队列
    /// </summary>
    public void Clear();
    /// <summary>
    /// 入队（即向队列尾部添加一个元素）
    /// </summary>
    /// <param name="item"></param>
    public void Enquene(T item);
    /// <summary>
    /// 出队(即从队列头部删除一个元素)
    /// </summary>
    /// <returns></returns>
    public T Dequene();
    /// <summary>
    /// 取得队列头部第一元素
    /// </summary>
    /// <returns></returns>
    public T Peek();
  }
}

下面是基于数组实现的示意图：

C#数据结构之队列(Quene)实例详解

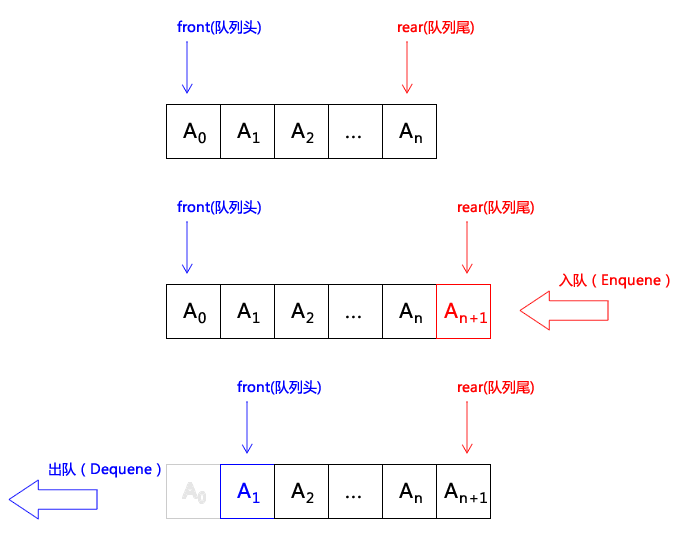
实现思路：用一个数组存放所有元素，同时设置二个关键变量front与rear用于记录队列“头”与“尾”的元素下标，当有元素入列时rear加1，当有元素出队时front+1，而rear-front即为队列实际元素的总数.

但有一种“队列伪满”的特殊情况要注意，如下图：

C#数据结构之队列(Quene)实例详解

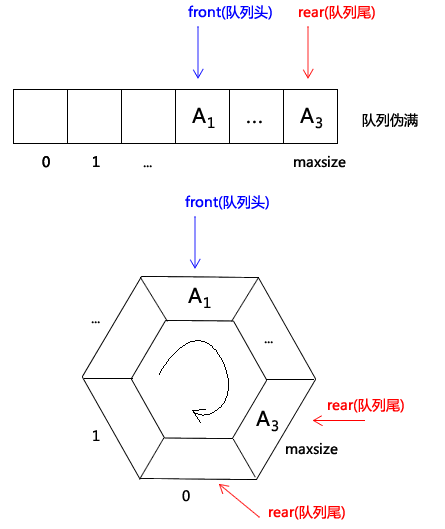
这张图上面的部分：假设经过入队、出队一番折腾后，rear已经指向数组的下标最大值，而front指向在中间(即front之间的元素已经出队不用考虑了，相当于front下标前面的内存区域空闲)，如果这时再有一个元素入列，rear+1就超出数组下标的最大值了，但是从图上一眼就能看出，实际上front前面还空着一堆位置可以重复利用，队列并非真正的“满”--这种情况称为伪满，为了解决这个问题，我们可以把数组想象为首尾相接的循环结构，即图中下面部分，这时候可以让rear重新指向到0，以便重复利用空闲的位置。

所以：入列时rear++的操作，应该稍做修正，当rear到数组下标最大值时，让它置0，以便能循环利用 (见后面的代码)

另外还有一个问题：最开始时front与rear都为-1，即front==rear时表示队列为空，改成循环以后，有可能会出现rear在循环过程中碰到front的情况，即真正意义的上"满"状态，这时rear也同样等于front，这样就无法单纯的用rear==front来判断是满，还是空？这时可以浪费一个元素的位置，认为当rear+1==front时，队列就已经满了，虽然牺牲了一个元素的空间，但却换来了逻辑的正确性，还是值得的。

完整实现如下：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
using System;
using System.Text;
namespace 栈与队列
{
  /// <summary>
  /// 循环顺序队列
  /// </summary>
  /// <typeparam name="T"></typeparam>
  public class CSeqQueue<T>:IQueue<T>
  {
    private int maxsize;
    private T[] data;
    private int front;
    private int rear;   
    public CSeqQueue(int size)
    {
      data = new T[size];
      maxsize = size;
      front = rear = -1;
    }
    public int Count()    
    {
      if (rear > front)
      {
        return rear - front;
      }
      else
      {
        return (rear - front + maxsize) % maxsize;
      }
    }
    public void Clear()
    {
      front = rear = -1;
    }
    public bool IsEmpty()
    {
      return front == rear;     
    }
    public bool IsFull()
    {     
      if (front != -1) //如果已经有元素出队过
      {
        return (rear + 1) % maxsize == front;//为了区分与IsEmpty的区别，有元素出队过以后，就只有浪费一个位置来保持逻辑正确性.
      }
      else
      {
        return rear == maxsize - 1;
      }     
    }
    public void Enqueue(T item)
    {
      if (IsFull())
      {
        Console.WriteLine("Queue is full");
        return;
      }
      if (rear == maxsize - 1) //如果rear到头了，则循环重来（即解决伪满问题）
      {
        rear = 0;
      }
      else
      {
        rear++;
      }
      data[rear] = item;
    }
    public T Dequeue()
    {     
      if (IsEmpty())
      {
        Console.WriteLine("Queue is empty");
        return default(T);
      }
      if (front == maxsize - 1) //如果front到头了，则重新置0
      {
        front = 0;
      }
      else
      {
        front++;
      }     
      return data[front];
    }
    public T Peek()
    {
      if (IsEmpty())
      {
        Console.WriteLine("Queue is empty!");
        return default(T);
      }
      return data[(front + 1) % maxsize];     
    }
    public override string ToString()
    {
      if (IsEmpty()) { return "queue is empty."; }
      StringBuilder sb = new StringBuilder();
      if (rear > front)
      {
        for (int i = front + 1; i <= rear; i++)
        {
          sb.Append(this.data[i].ToString() + ",");
        }
      }
      else
      {
        for (int i = front + 1; i < maxsize; i++)
        {
          sb.Append(this.data[i].ToString() + ",");
        }
        for (int i = 0; i <= rear; i++)
        {
          sb.Append(this.data[i].ToString() + ",");
        }
      }
      return "front = " + this.front + " \t rear = " + this.rear + "\t count = " + this.Count() + "\t data = " + sb.ToString().Trim(',');
    }
  }
}

测试代码片段：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
CSeqQueue<int> queue = new CSeqQueue<int>(5);
queue.Enqueue(1);
queue.Enqueue(2);
queue.Enqueue(3);
queue.Enqueue(4);
Console.WriteLine(queue);//front = -1    rear = 3    count = 4    data = 1,2,3,4
queue.Dequeue();
Console.WriteLine(queue);//front = 0    rear = 3    count = 3    data = 2,3,4
queue.Dequeue();
Console.WriteLine(queue);//front = 1    rear = 3    count = 2    data = 3,4
queue.Enqueue(5);
Console.WriteLine(queue);//front = 1    rear = 4    count = 3    data = 3,4,5
queue.Enqueue(6);
Console.WriteLine(queue);//front = 1    rear = 0    count = 4    data = 3,4,5,6
queue.Enqueue(7);    //Queue is full
Console.WriteLine(queue);//front = 1    rear = 0    count = 4    data = 3,4,5,6
queue.Dequeue();
queue.Enqueue(7);
Console.WriteLine(queue);//front = 2    rear = 1    count = 4    data = 4,5,6,7
queue.Clear();
Console.WriteLine(queue);//queue is empty.
queue.Enqueue(1);
queue.Enqueue(2);
queue.Enqueue(3);
queue.Enqueue(4);
Console.WriteLine(queue);//front = -1    rear = 3    count = 4    data = 1,2,3,4
queue.Enqueue(5);
Console.WriteLine(queue);//front = -1    rear = 4    count = 5    data = 1,2,3,4,5
queue.Enqueue(6);    //Queue is full
Console.WriteLine(queue);//front = -1    rear = 4    count = 5    data = 1,2,3,4,5
queue.Dequeue();
queue.Dequeue();
queue.Dequeue();
queue.Dequeue();
Console.WriteLine(queue);//front = 3    rear = 4    count = 1    data = 5
queue.Dequeue();
Console.WriteLine(queue);//queue is empty.
queue.Enqueue(0);
queue.Enqueue(1);
queue.Enqueue(2);
queue.Enqueue(3);
queue.Enqueue(4);    //Queue is full
Console.WriteLine(queue);//front = 4    rear = 3    count = 4    data = 0,1,2,3
Console.WriteLine(queue.Peek());//0
queue.Dequeue();
Console.WriteLine(queue);//front = 0    rear = 3    count = 3    data = 1,2,3
queue.Dequeue();
Console.WriteLine(queue);//front = 1    rear = 3    count = 2    data = 2,3
queue.Dequeue();
Console.WriteLine(queue);//front = 2    rear = 3    count = 1    data = 3
queue.Dequeue();
Console.WriteLine(queue);//queue is empty.
queue.Enqueue(9);
Console.WriteLine(queue);//front = 3    rear = 4    count = 1    data = 9
Console.ReadLine();

当然，队列也可以用链表来实现，相对要容易很多。

先定义链表中的节点Node.cs

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
namespace 栈与队列
{
  public class Node<T>
  {
    private T data;
    private Node<T> next;
    public Node(T data, Node<T> next)
    {
      this.data = data;
      this.next = next;
    }
    public Node(Node<T> next)
    {
      this.next = next;
      this.data = default(T);
    }
    public Node(T data)
    {
      this.data = data;
      this.next = null;
    }
    public Node()
    {
      this.data = default(T);
      this.next = null;
    }
    public T Data {
      get { return this.data; }
      set { this.data = value; }
    }
    public Node<T> Next
    {
      get { return next; }
      set { next = value; }
    }
  }
}

为了方便，定义了很多构造函数的重载版本，当然这些只是浮云，重点是理解结构：data用来保存数据，next指出下一个节点是谁
链式队列的完整实现LinkQueue.cs

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
using System;
using System.Text;
namespace 栈与队列
{
  public class LinkQueue:IQueue
  {
    private Node front;//队列头
    private Node rear;//队列尾
    private int num;//队列元素个数
    ///
    /// 构造器
    ///
    public LinkQueue()
    {
      //初始时front,rear置为null，num置0
      front = rear = null;
      num = 0;
    }
    public int Count()
    {
      return this.num;
    }
    public void Clear()
    {
      front = rear = null;
      num = 0;
    }
    public bool IsEmpty()
    {
      return (front == rear && num == 0);
    }
    //入队
    public void Enqueue(T item)
    {
      Node q = new Node(item);
      if (rear == null)//第一个元素入列时
      {
        front = rear = q;
      }
      else
      {
        //把新元素挂到链尾
        rear.Next = q;
        //修正rear指向为最后一个元素
        rear = q;
      }
      //元素总数+1
      num++;
    }
    //出队
    public T Dequeue()
    {
      if (IsEmpty())
      {
        Console.WriteLine("Queue is empty!");
        return default(T);
      }
      //取链首元素
      Node p = front;
      //链头指向后移一位
      front = front.Next;
      //如果此时链表为空，则同步修正rear
      if (front == null)
      {
        rear = null;
      }
      num--;//个数-1
      return p.Data;
    }
    public T Peek()
    {
      if (IsEmpty())
      {
        Console.WriteLine("Queue is empty!");
        return default(T);
      }
      return front.Data;
    }
    public override string ToString()
    {
      if (IsEmpty()) {
        Console.WriteLine("Queue is empty!");
      }
      StringBuilder sb = new StringBuilder();
      Node node = front;
      sb.Append(node.Data.ToString());
      while (node.Next!=null)
      {
        sb.Append("," + node.Next.Data.ToString());
        node = node.Next;
      }
      return sb.ToString().Trim(',');
    }
  }
}

希望本文所述对大家C#程序设计有所帮助。

  • 数据结构
  • C#
  • 队列
  • Quene

    • 延伸 · 阅读

    精彩推荐
    • C#三十分钟快速掌握C# 6.0知识点

      三十分钟快速掌握C# 6.0知识点

      这篇文章主要介绍了C# 6.0的相关知识点，文中介绍的非常详细，通过这篇文字可以让大家在三十分钟内快速的掌握C# 6.0，需要的朋友可以参考借鉴，下面来...

      雨夜潇湘8272021-12-28
    • C#VS2012 程序打包部署图文详解

      VS2012 程序打包部署图文详解

      VS2012虽然没有集成打包工具，但它为我们提供了下载的端口，需要我们手动安装一个插件InstallShield。网上有很多第三方的打包工具，但为什么偏要使用微软...

      张信秀7712021-12-15
    • C#如何使用C#将Tensorflow训练的.pb文件用在生产环境详解

      如何使用C#将Tensorflow训练的.pb文件用在生产环境详解

      这篇文章主要给大家介绍了关于如何使用C#将Tensorflow训练的.pb文件用在生产环境的相关资料，文中通过示例代码介绍的非常详细，需要的朋友可以参考借鉴...

      bbird201811792022-03-05
    • C#C#微信公众号与订阅号接口开发示例代码

      C#微信公众号与订阅号接口开发示例代码

      这篇文章主要介绍了C#微信公众号与订阅号接口开发示例代码,结合实例形式简单分析了C#针对微信接口的调用与处理技巧,需要的朋友可以参考下...

      smartsmile20127762021-11-25
    • C#SQLite在C#中的安装与操作技巧

      SQLite在C#中的安装与操作技巧

      SQLite，是一款轻型的数据库，用于本地的数据储存。其优点有很多，下面通过本文给大家介绍SQLite在C#中的安装与操作技巧，感兴趣的的朋友参考下吧...

      蓝曈魅11162022-01-20
    • C#C#设计模式之Strategy策略模式解决007大破密码危机问题示例

      C#设计模式之Strategy策略模式解决007大破密码危机问题示例

      这篇文章主要介绍了C#设计模式之Strategy策略模式解决007大破密码危机问题,简单描述了策略模式的定义并结合加密解密算法实例分析了C#策略模式的具体使用...

      GhostRider10972022-01-21
    • C#深入理解C#的数组

      深入理解C#的数组

      本篇文章主要介绍了C#的数组，数组是一种数据结构，详细的介绍了数组的声明和访问等，有兴趣的可以了解一下。...

      佳园9492021-12-10
    • C#利用C#实现网络爬虫

      利用C#实现网络爬虫

      这篇文章主要介绍了利用C#实现网络爬虫，完整的介绍了C#实现网络爬虫详细过程，感兴趣的小伙伴们可以参考一下...

      C#教程网11852021-11-16
    最近更新
    编辑推荐
    阅读排行
    热门标签
    物体颜色 　 osg 　 刷新桌面 　 nancy 　 TaskManager 　 网站授权 　 下拉式 　 DirectoryEntry 　 C#编程 　 网站功能 　 通知窗口 　 相互关系 　 语句顺序 　 编程错误 　 悬浮框 　 Dispose 　 滚动新闻 　 HttpPost 　 静态构造函数 　 焦点 　 类型派生 　 深度拷贝 　 小写转大写金额 　 任务并行库 　 众数 　 更新数据库 　 统计字数 　 二乘法 　 IComparer 　 DataBinding 　
    © 2019-2023 服务器之家(www.zzvips.com) 版权所有关于我们联系我们版权申明网站地图