路径:
https://pytorch.org/docs/master/nn.init.html#nn-init-doc
初始化函数:torch.nn.init
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
|
# -*- coding: utf-8 -*-"""created on 2019@author: fancp"""import torch import torch.nn as nnw = torch.empty(3,5)#1.均匀分布 - u(a,b)#torch.nn.init.uniform_(tensor, a=0.0, b=1.0)print(nn.init.uniform_(w))# =============================================================================# tensor([[0.9160, 0.1832, 0.5278, 0.5480, 0.6754],# [0.9509, 0.8325, 0.9149, 0.8192, 0.9950],# [0.4847, 0.4148, 0.8161, 0.0948, 0.3787]])# =============================================================================#2.正态分布 - n(mean, std)#torch.nn.init.normal_(tensor, mean=0.0, std=1.0)print(nn.init.normal_(w))# =============================================================================# tensor([[ 0.4388, 0.3083, -0.6803, -1.1476, -0.6084],# [ 0.5148, -0.2876, -1.2222, 0.6990, -0.1595],# [-2.0834, -1.6288, 0.5057, -0.5754, 0.3052]])# =============================================================================#3.常数 - 固定值 val#torch.nn.init.constant_(tensor, val)print(nn.init.constant_(w, 0.3))# =============================================================================# tensor([[0.3000, 0.3000, 0.3000, 0.3000, 0.3000],# [0.3000, 0.3000, 0.3000, 0.3000, 0.3000],# [0.3000, 0.3000, 0.3000, 0.3000, 0.3000]])# =============================================================================#4.全1分布#torch.nn.init.ones_(tensor)print(nn.init.ones_(w))# =============================================================================# tensor([[1., 1., 1., 1., 1.],# [1., 1., 1., 1., 1.],# [1., 1., 1., 1., 1.]])# =============================================================================#5.全0分布#torch.nn.init.zeros_(tensor)print(nn.init.zeros_(w))# =============================================================================# tensor([[0., 0., 0., 0., 0.],# [0., 0., 0., 0., 0.],# [0., 0., 0., 0., 0.]])# =============================================================================#6.对角线为 1,其它为 0#torch.nn.init.eye_(tensor)print(nn.init.eye_(w))# =============================================================================# tensor([[1., 0., 0., 0., 0.],# [0., 1., 0., 0., 0.],# [0., 0., 1., 0., 0.]])# =============================================================================#7.xavier_uniform 初始化#torch.nn.init.xavier_uniform_(tensor, gain=1.0)#from - understanding the difficulty of training deep feedforward neural networks - bengio 2010print(nn.init.xavier_uniform_(w, gain=nn.init.calculate_gain('relu')))# =============================================================================# tensor([[-0.1270, 0.3963, 0.9531, -0.2949, 0.8294],# [-0.9759, -0.6335, 0.9299, -1.0988, -0.1496],# [-0.7224, 0.2181, -1.1219, 0.8629, -0.8825]])# =============================================================================#8.xavier_normal 初始化#torch.nn.init.xavier_normal_(tensor, gain=1.0)print(nn.init.xavier_normal_(w))# =============================================================================# tensor([[ 1.0463, 0.1275, -0.3752, 0.1858, 1.1008],# [-0.5560, 0.2837, 0.1000, -0.5835, 0.7886],# [-0.2417, 0.1763, -0.7495, 0.4677, -0.1185]])# =============================================================================#9.kaiming_uniform 初始化#torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')#from - delving deep into rectifiers: surpassing human-level performance on imagenet classification - hekaiming 2015print(nn.init.kaiming_uniform_(w, mode='fan_in', nonlinearity='relu'))# =============================================================================# tensor([[-0.7712, 0.9344, 0.8304, 0.2367, 0.0478],# [-0.6139, -0.3916, -0.0835, 0.5975, 0.1717],# [ 0.3197, -0.9825, -0.5380, -1.0033, -0.3701]])# =============================================================================#10.kaiming_normal 初始化#torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')print(nn.init.kaiming_normal_(w, mode='fan_out', nonlinearity='relu'))# =============================================================================# tensor([[-0.0210, 0.5532, -0.8647, 0.9813, 0.0466],# [ 0.7713, -1.0418, 0.7264, 0.5547, 0.7403],# [-0.8471, -1.7371, 1.3333, 0.0395, 1.0787]])# =============================================================================#11.正交矩阵 - (semi)orthogonal matrix#torch.nn.init.orthogonal_(tensor, gain=1)#from - exact solutions to the nonlinear dynamics of learning in deep linear neural networks - saxe 2013print(nn.init.orthogonal_(w))# =============================================================================# tensor([[-0.0346, -0.7607, -0.0428, 0.4771, 0.4366],# [-0.0412, -0.0836, 0.9847, 0.0703, -0.1293],# [-0.6639, 0.4551, 0.0731, 0.1674, 0.5646]])# =============================================================================#12.稀疏矩阵 - sparse matrix #torch.nn.init.sparse_(tensor, sparsity, std=0.01)#from - deep learning via hessian-free optimization - martens 2010print(nn.init.sparse_(w, sparsity=0.1))# =============================================================================# tensor([[ 0.0000, 0.0000, -0.0077, 0.0000, -0.0046],# [ 0.0152, 0.0030, 0.0000, -0.0029, 0.0005],# [ 0.0199, 0.0132, -0.0088, 0.0060, 0.0000]])# ============================================================================= |
补充:【pytorch参数初始化】 pytorch默认参数初始化以及自定义参数初始化
本文用两个问题来引入
1.pytorch自定义网络结构不进行参数初始化会怎样,参数值是随机的吗?
2.如何自定义参数初始化?
先回答第一个问题
在pytorch中,有自己默认初始化参数方式,所以在你定义好网络结构以后,不进行参数初始化也是可以的。
1.conv2d继承自_convnd,在_convnd中,可以看到默认参数就是进行初始化的,如下图所示
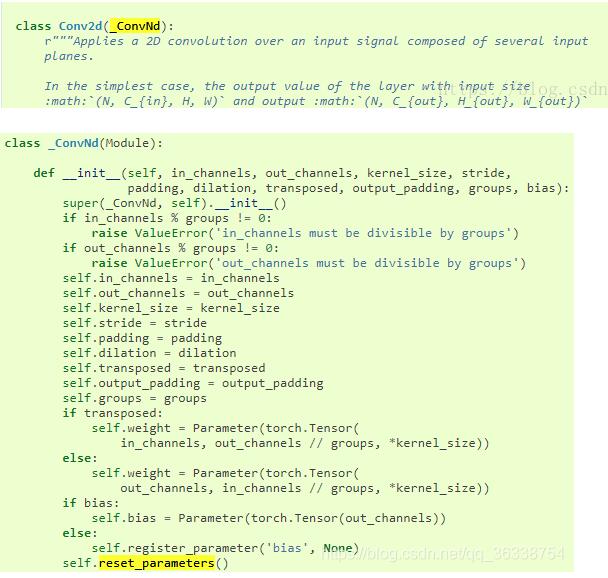

2.torch.nn.batchnorm2d也一样有默认初始化的方式
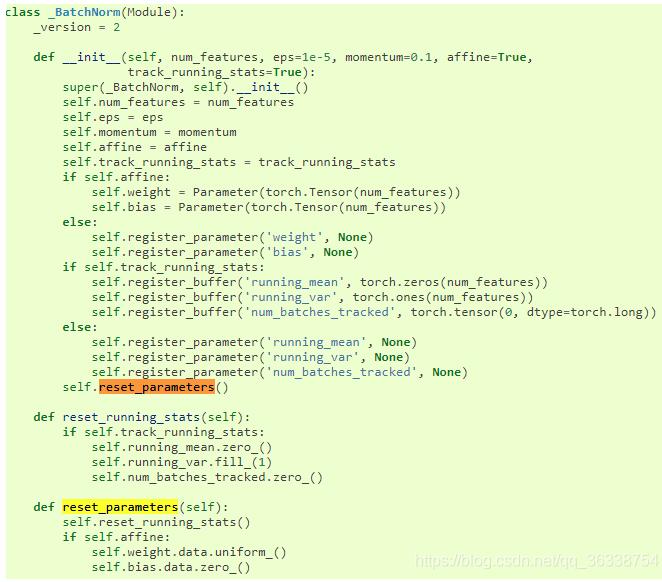
3.torch.nn.linear也如此

现在来回答第二个问题。
pytorch中对神经网络模型中的参数进行初始化方法如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
from torch.nn import init#define the initial function to init the layer's parameters for the networkdef weigth_init(m): if isinstance(m, nn.conv2d): init.xavier_uniform_(m.weight.data) init.constant_(m.bias.data,0.1) elif isinstance(m, nn.batchnorm2d): m.weight.data.fill_(1) m.bias.data.zero_() elif isinstance(m, nn.linear): m.weight.data.normal_(0,0.01) m.bias.data.zero_() |
首先定义了一个初始化函数,接着进行调用就ok了,不过要先把网络模型实例化:
|
1
2
3
|
#define network model = net(args.input_channel,args.output_channel) model.apply(weigth_init) |
此上就完成了对模型中训练参数的初始化。
在知乎上也有看到一个类似的版本,也相应的贴上来作为参考了:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def initnetparams(net): '''init net parameters.''' for m in net.modules(): if isinstance(m, nn.conv2d): init.xavier_uniform(m.weight) if m.bias: init.constant(m.bias, 0) elif isinstance(m, nn.batchnorm2d): init.constant(m.weight, 1) init.constant(m.bias, 0) elif isinstance(m, nn.linear): init.normal(m.weight, std=1e-3) if m.bias: init.constant(m.bias, 0) initnetparams(net) |
再说一下关于模型的保存及加载
1.保存有两种方式,第一种是保存模型的整个结构信息和参数,第二种是只保存模型的参数
|
1
2
3
4
5
|
#保存整个网络模型及参数torch.save(net, 'net.pkl') #仅保存模型参数torch.save(net.state_dict(), 'net_params.pkl') |
2.加载对应保存的两种网络
|
1
2
3
4
5
6
7
|
# 保存和加载整个模型 torch.save(model_object, 'model.pth') model = torch.load('model.pth') # 仅保存和加载模型参数 torch.save(model_object.state_dict(), 'params.pth') model_object.load_state_dict(torch.load('params.pth')) |
以上为个人经验,希望能给大家一个参考,也希望大家多多支持服务器之家。如有错误或未考虑完全的地方,望不吝赐教。
原文链接:https://blog.csdn.net/u013841196/article/details/102832744










