蒙特卡罗方法是一种统计模拟方法,由冯·诺依曼和乌拉姆提出,在大量的随机数下,根据概率估计结果,随机数据越多,获得的结果越精确。下面我们将用python实现蒙特卡罗方法。
1.首先我们做一个简单的圆周率的近似计算,在这个过程中我们要用到随机数,因此需要先使用import numpy as np导入numpy库。
2.代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import numpy as np total = 8000000count = 0 for i in range(total): x = np.random.rand() y = np.random.rand() dis = (x**2+y**2)**0.5 if dis <= 1: count = count+1pi = 4*count/totalprint(pi) |
3.在上面的程序中我们用8000000个随机数进行投放,这样得到的结果会更精确一些,运行程序需要一定的时间,最终得到的结果如下
4.下面我们进行一项简单的应用,下图为我在画图工具中随便画的一个图,我们可以用蒙特卡罗方法来估算图中黑色部分的面积。

5.上面的图形是不规则的,我们只需知道在投放大量随机数的情况下,随机数在黑色部分出现的概率,再用总面积相乘即可估算黑色部分的面积。我们知道,黑色的rgb编码为(0,0,0),所以需要统计rgb编码为(0,0,0)时随机数的投放概率即可。
6.代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
from pil import imageimport numpy as np im = image.open("c:/users/21974/desktop/handwrite2.png")total = 9000000count = 0defin = 0width = im.size[0]height = im.size[1] for i in range(total): #用蒙特卡罗方法获得估计值 x = np.random.randint(0, width-1) y = np.random.randint(0, height-1) k = im.getpixel((x, y)) if k[0]+k[1]+k[2] == 0: count += 1print(int(width*height*count/total)) for i in range(width): #用遍历获得准确值 for j in range(height): k = im.getpixel((i, j)) if k[0] + k[1] + k[2] == 0: defin += 1print(defin) |
上面的代码可分为两部分,第一个for后面是用蒙特卡罗方法获得的面积的估计值,第二个for后面是用遍历所有像素点的方法获得的面积的精确值,获得两个输出后进行对比。
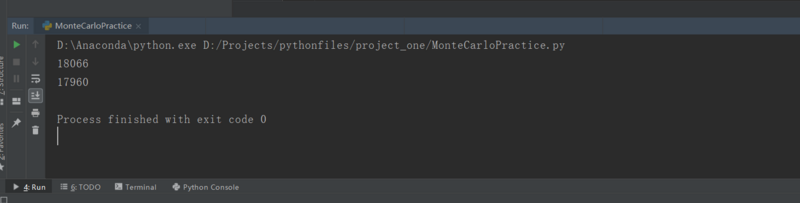
我们在上面的程序中采用了9000000个随机数,可以看出两个输出结果相差并不大。










