起步
这是一个相当实用的内置模块,但是很多人竟然不知道他的存在——笔者也是今天偶然看到的,哎……尽管如此,还是改变不了这个模块好用的事实
heapq 模块实现了适用于python列表的最小堆排序算法。
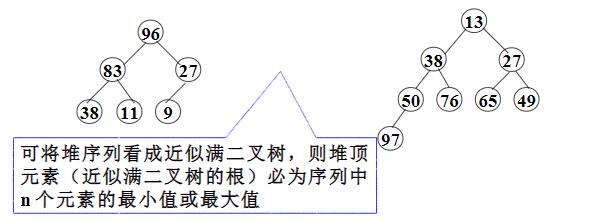
堆是一个树状的数据结构,其中的子节点都与父母排序顺序关系。因为堆排序中的树是满二叉树,因此可以用列表来表示树的结构,使得元素 n 的子元素位于 2n + 1 和 2n + 2 的位置(对于从零开始的索引)。
本文内容将分为三个部分,第一个部分简单介绍 heapq 模块的使用;第二部分回顾堆排序算法;第三部分分析heapq中的实现。
heapq 的使用
创建堆有两个基本的方法:heappush() 和 heapify(),取出堆顶元素用 heappop()。
heappush() 是用来向已有的堆中添加元素,一般从空列表开始构建:
|
1
2
3
4
5
6
7
8
9
10
|
import heapqdata = [97, 38, 27, 50, 76, 65, 49, 13]heap = []for n in data: heapq.heappush(heap, n)print('pop:', heapq.heappop(heap)) # pop: 13print(heap) # [27, 50, 38, 97, 76, 65, 49] |
如果数据已经在列表中,则使用 heapify() 进行重排:
|
1
2
3
4
5
6
7
8
|
import heapqdata = [97, 38, 27, 50, 76, 65, 49, 13]heapq.heapify(data)print('pop:', heapq.heappop(data)) # pop: 13print(data) # [27, 38, 49, 50, 76, 65, 97] |
回顾堆排序算法
堆排序算法基本思想是:将无序序列建成一个堆,得到关键字最小(或最大的记录;输出堆顶的最小 (大)值后,使剩余的 n-1 个元素 重又建成一个堆,则可得到n个元素的次小值 ;重复执行,得到一个有序序列,这个就是堆排序的过程。
堆排序需要解决两个问题:
- 如何由一个无序序列建立成一个堆?
- 如何在输出堆顶元素之后,调整剩余元素,使之成为一个新的堆?
- 新添加元素和,如何调整堆?
先来看看第二个问题的解决方法。采用的方法叫“筛选”,当输出堆顶元素之后,就将堆中最后一个元素代替之;然后将根结点值与左、右子树的根结点值进行比较 ,并与其中小者进行交换;重复上述操作,直至叶子结点,将得到新的堆,称这个从堆顶至叶子的调整过程为“筛选”。
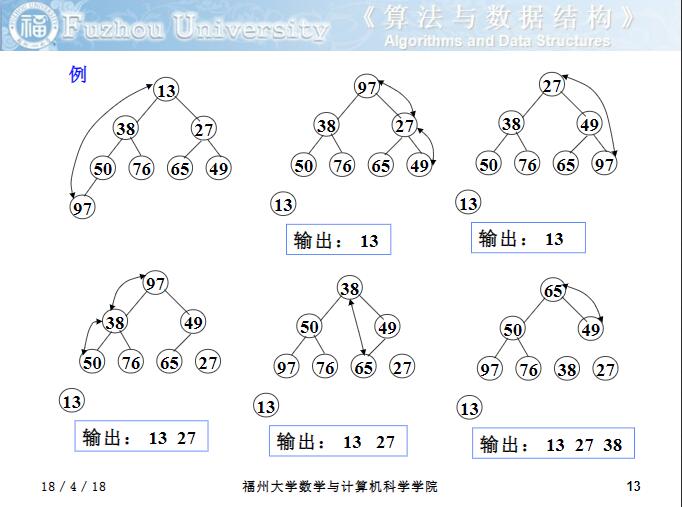
如上图所示,当堆顶 13 输出后,将堆中末尾的 97 替代为堆顶,然后堆顶与它的子节点 38 和 27 中的小者交换;元素 97 在新的位置上在和它的子节点 65 和 49 中的小者交换;直到元素97成为叶节点,就得到了新的堆。这个过程也叫 下沉 。
让堆中位置为 pos 元素进行下沉的如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
def heapdown(heap, pos): endpos = len(heap) while pos < endpos: lchild = 2 * pos + 1 rchild = 2 * pos + 2 if lchild >= endpos: # 如果pos已经是叶节点,退出循环 break childpos = lchild # 假设要交换的节点是左节点 if rchild < endpos and heap[childpos] > heap[rchild]: childpos = rchild if heap[pos] < heap[childpos]: # 如果节点比子节点都小,退出循环 break heap[pos], heap[childpos] = heap[childpos], heap[pos] # 交换 pos = childpos |
再来看看如何解决第三个问题:新添加元素和,如何调整堆?这个的方法正好与 下沉 相反,首先将新元素放置列表的最后,然后新元素与其父节点比较,若比父节点小,与父节点交换;重复过程直到比父节点大或到根节点。这个过程使得元素从底部不断上升,从下至上恢复堆的顺序,称为 上浮 。
将位置为 pos 进行上浮的代码为:
|
1
2
3
4
5
6
7
8
|
def heapup(heap, startpos, pos): # 如果是新增元素,startpos 传入 0 while pos > startpos: parentpos = (pos - 1) // 2 if heap[pos] < heap[parentpos]: heap[pos], heap[parentpos] = heap[parentpos], heap[pos] pos = parentpos else: break |
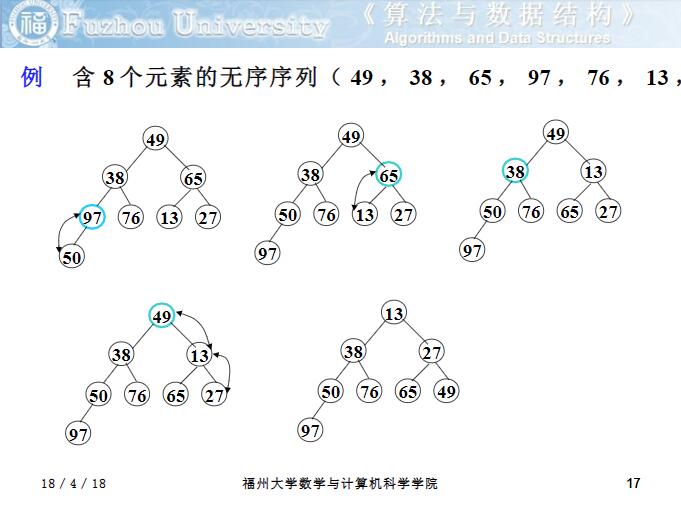
第一个问题:如何由一个无序序列建立成一个堆?从无序序列的第 n/2 个元素 (即此无序序列对应的完全二叉树的最后一个非终端结点 )起 ,至第一个元素止,依次进行下沉:
|
1
2
|
for i in reversed(range(len(data) // 2)): heapdown(data, i) |
heapq 源码分析
添加新元素到堆中的 heappush() 函数:
|
1
2
3
4
|
def heappush(heap, item): """push item onto heap, maintaining the heap invariant.""" heap.append(item) _siftdown(heap, 0, len(heap)-1) |
把目标元素放置列表最后,然后进行上浮。尽管它命名叫 down ,但这个过程是上浮的过程,这个命名也让我困惑,后来我才知道它是因为元素的索引不断减小,所以命名 down 。下沉的过程它也就命名为 up 了。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
def _siftdown(heap, startpos, pos): newitem = heap[pos] # follow the path to the root, moving parents down until finding a place # newitem fits. while pos > startpos: parentpos = (pos - 1) >> 1 parent = heap[parentpos] if newitem < parent: heap[pos] = parent pos = parentpos continue break heap[pos] = newitem |
一样是通过 newitem 不断与父节点比较。不一样的是这里缺少了元素交换的过程,而是计算出新元素最后所在的位置 pos 并进行的赋值。显然这是优化后的代码,减少了不断交换元素的冗余过程。
再来看看输出堆顶元素的函数 heappop():
|
1
2
3
4
5
6
7
8
9
|
def heappop(heap): """pop the smallest item off the heap, maintaining the heap invariant.""" lastelt = heap.pop() # raises appropriate indexerror if heap is empty if heap: returnitem = heap[0] heap[0] = lastelt _siftup(heap, 0) return returnitem return lastelt |
通过 heap.pop() 获得列表中的最后一个元素,然后替换为堆顶 heap[0] = lastelt ,再进行下沉:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
def _siftup(heap, pos): endpos = len(heap) startpos = pos newitem = heap[pos] # bubble up the smaller child until hitting a leaf. childpos = 2*pos + 1 # 左节点,默认替换左节点 while childpos < endpos: # set childpos to index of smaller child. rightpos = childpos + 1 # 右节点 if rightpos < endpos and not heap[childpos] < heap[rightpos]: childpos = rightpos # 当右节点比较小时,应交换的是右节点 # move the smaller child up. heap[pos] = heap[childpos] pos = childpos childpos = 2*pos + 1 # the leaf at pos is empty now. put newitem there, and bubble it up # to its final resting place (by sifting its parents down). heap[pos] = newitem _siftdown(heap, startpos, pos) |
这边的代码将准备要下沉的元素视为新元素 newitem ,将其当前的位置 pos 视为空位置,由其子节点中的小者进行取代,反复如此,最后会在叶节点留出一个位置,这个位置放入 newitem ,再让新元素进行上浮。
再来看看让无序数列重排成堆的 heapify() 函数:
|
1
2
3
4
5
|
def heapify(x): """transform list into a heap, in-place, in o(len(x)) time.""" n = len(x) for i in reversed(range(n//2)): _siftup(x, i) |
这部分就和理论上的一致,从最后一个非叶节点 (n // 2) 到根节点为止,进行下沉。
总结
堆排序结合图来理解还是比较好理解的。这种数据结构常用于优先队列(标准库queue的优先队列用的就是堆)。 heapq 模块中还有很多其他 heapreplace ,heappushpop 等大体上都很类似。
好了,以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,如果有疑问大家可以留言交流,谢谢大家对服务器之家的支持。
原文链接:http://www.hongweipeng.com/index.php/archives/1716/










