本文实例讲述了Python实现的线性回归算法。分享给大家供大家参考,具体如下:
用python实现线性回归
Using Python to Implement Line Regression Algorithm
小菜鸟记录学习过程
代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
#encoding:utf-8""" Author: njulpy Version: 1.0 Data: 2018/04/09 Project: Using Python to Implement LineRegression Algorithm"""import numpy as npimport pandas as pdfrom numpy.linalg import invfrom numpy import dotfrom sklearn.model_selection import train_test_splitimport matplotlib.pyplot as pltfrom sklearn import linear_model# 最小二乘法def lms(x_train,y_train,x_test): theta_n = dot(dot(inv(dot(x_train.T, x_train)), x_train.T), y_train) # theta = (X'X)^(-1)X'Y #print(theta_n) y_pre = dot(x_test,theta_n) mse = np.average((y_test-y_pre)**2) #print(len(y_pre)) #print(mse) return theta_n,y_pre,mse#梯度下降算法def train(x_train, y_train, num, alpha,m, n): beta = np.ones(n) for i in range(num): h = np.dot(x_train, beta) # 计算预测值 error = h - y_train.T # 计算预测值与训练集的差值 delt = 2*alpha * np.dot(error, x_train)/m # 计算参数的梯度变化值 beta = beta - delt #print('error', error) return betaif __name__ == "__main__": iris = pd.read_csv('iris.csv') iris['Bias'] = float(1) x = iris[['Sepal.Width', 'Petal.Length', 'Petal.Width', 'Bias']] y = iris['Sepal.Length'] x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=5) t = np.arange(len(x_test)) m, n = np.shape(x_train) # Leastsquare theta_n, y_pre, mse = lms(x_train, y_train, x_test) # plt.plot(t, y_test, label='Test') # plt.plot(t, y_pre, label='Predict') # plt.show() # GradientDescent beta = train(x_train, y_train, 1000, 0.001, m, n) y_predict = np.dot(x_test, beta.T) # plt.plot(t, y_predict) # plt.plot(t, y_test) # plt.show() # sklearn regr = linear_model.LinearRegression() regr.fit(x_train, y_train) y_p = regr.predict(x_test) print(regr.coef_,theta_n,beta) l1,=plt.plot(t, y_predict) l2,=plt.plot(t, y_p) l3,=plt.plot(t, y_pre) l4,=plt.plot(t, y_test) plt.legend(handles=[l1, l2,l3,l4 ], labels=['GradientDescent', 'sklearn','Leastsquare','True'], loc='best') plt.show() |
输出结果
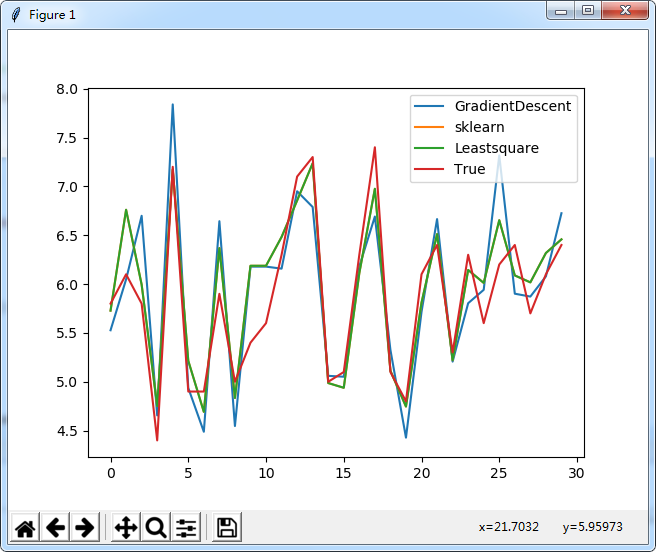
sklearn: [ 0.65368836 0.70955523 -0.54193454 0. ]
LeastSquare: [ 0.65368836 0.70955523 -0.54193454 1.84603897]
GradientDescent: [ 0.98359285 0.29325906 0.60084232 1.006859 ]
附:上述示例中的iris.csv文件点击此处本站下载。
希望本文所述对大家Python程序设计有所帮助。
原文链接:https://blog.csdn.net/njulpy/article/details/79899740










