平衡二叉树:
在上一节二叉树的基础上我们实现,如何将生成平衡的二叉树
所谓平衡二叉树:
我自己定义就是:任何一个节点的左高度和右高度的差的绝对值都小于2
如图所示,此时a的左高度等于3,有高度等于1,差值为2,属于不平衡中的左偏
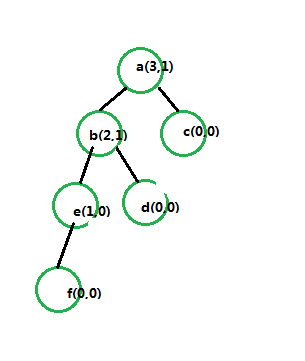
此时的处理办法就是:
将不平衡的元素的左枝的最右节点变为当前节点,
此时分两种情况:
一、左枝有最右节点
将最右节点的左枝赋予其父节点的右枝
二、左枝没有最右节点,
直接将左枝节点做父级节点,父级节点做其右枝
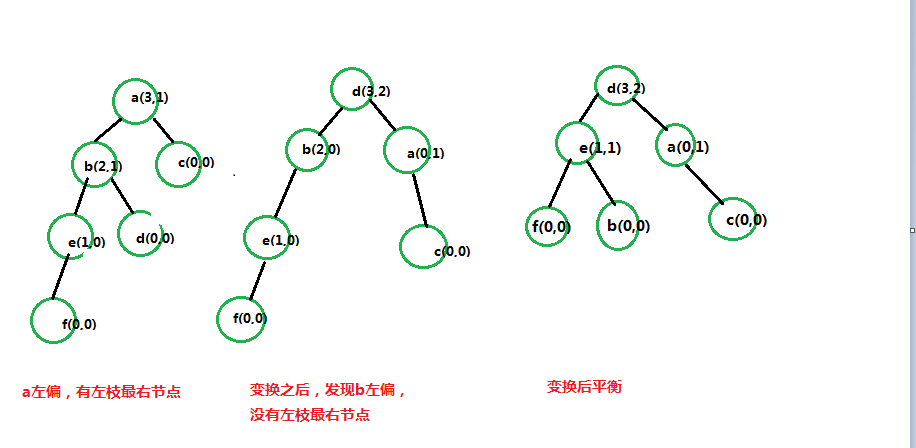
如图所示,图更清楚些。
可能会有疑问,为什么这样变换?
假定a左偏,就需要一个比a小的最少一个值d(因为d唯一 一个是比a小,而且比a的左枝所有数都大的值)做父集结点,a做d的右枝,这样在最上面的d节点就平衡了。
我们可以反证一下:
如果不是d是另一个数假设为h,此时h做父节点,a做父节点的右节点
因为a在h右边,所以 a > h
因为b,e,d,f都是h的左枝,所以 h>d>b>e>f
所以 a>h>d>b>e>f
所以在不加入新节点的情况下,就只能是d
左偏和右偏是一样的,可以完全镜像过来就ok了
处理了所有节点 的左偏和右偏使整个二叉树平衡,这就是平衡二叉树的基本思想
代码实现:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
|
# -*- coding:utf-8 -*-# 日期:2018/6/12 8:37# author:小鼠标# 节点对象class node: def __init__(self): self.left_children = none self.left_height = 0 self.right_children = none self.right_height = 0 self.value = none# 二叉树对象class tree: def __init__(self): self.root = false self.front_list = [] self.middle_list = [] self.after_list = [] # 生成二叉树 def create_tree(self,n=0,l=[]): if l == []: print("传入的列表为空") return if n > len(l)-1: print("二叉树生成") return node = node() node.value = l[n] if not self.root: self.root = node self.list = l else: self.add(self.root,node) self.create_tree(n+1,l) # 添加节点 def add(self,parent,new_node): if new_node.value > parent.value: # 插入值比父亲值大,所以在父节点右边 if parent.right_children == none: parent.right_children = new_node # 新插入节点的父亲节点的高度值为1,也就是子高度值0+1 parent.right_height = 1 # 插入值后 从下到上更新节点的height else: self.add(parent.right_children,new_node) # 父亲节点的右高度等于右孩子,左右高度中较大的值 + 1 parent.right_height = max(parent.right_children.right_height, parent.right_children.left_height) + 1 # ======= 此处开始判断平衡二叉树======= # 右边高度大于左边高度 属于右偏 if parent.right_height - parent.left_height >= 2: self.right_avertence(parent) else: # 插入值比父亲值小,所以在父节点左边 if parent.left_children == none: parent.left_children = new_node parent.left_height = 1 else: self.add(parent.left_children,new_node) parent.left_height = max(parent.left_children.right_height, parent.left_children.left_height) + 1 # ======= 此处开始判断平衡二叉树======= # 左边高度大于右边高度 属于左偏 if parent.left_height - parent.right_height >= 2: self.left_avertence(parent) # 更新当前节点下的所有节点的高度 def update_height(self,node): # 初始化节点高度值为0 node.left_height = 0 node.right_height = 0 # 是否到最底层的一个 if node.left_children == none and node.right_children == none: return else: if node.left_children: self.update_height(node.left_children) # 当前节点的高度等于左右子节点高度的较大值 + 1 node.left_height = max(node.left_children.left_height,node.left_children.right_height) + 1 if node.right_children: self.update_height(node.right_children) # 当前节点的高度等于左右子节点高度的较大值 + 1 node.right_height = max(node.right_children.left_height, node.right_children.right_height) + 1 # 检查是否仍有不平衡 if node.left_height - node.right_height >= 2: self.left_avertence(node) elif node.left_height - node.right_height <= -2: self.right_avertence(node) def right_avertence(self,node): # 右偏 就将当前节点的最左节点做父亲 new_code = node() new_code.value = node.value new_code.left_children = node.left_children best_left = self.best_left_right(node.right_children) v = node.value # 返回的对象本身, if best_left == node.right_children and best_left.left_children == none: # 说明当前节点没有有节点 node.value = best_left.value node.right_children = best_left.right_children else: node.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children node.left_children = new_code self.update_height(node) # 处理左偏情况 def left_avertence(self,node): new_code = node() new_code.value = node.value new_code.right_children = node.right_children best_right = self.best_left_right(node.left_children,1) v = node.value # 返回的对象本身, if best_right == node.left_children and best_right.right_children == none: # 说明当前节点没有有节点 node.value = best_right.value node.left_children = best_right.left_children else: node.value = best_right.right_children.value best_right.right_children = best_right.right_children.left_children node.right_children = new_code self.update_height(node) # 返回node节点最左(右)子孙的父级 def best_left_right(self,node,type=0): # type=0 默认找最左子孙 if type == 0: if node.left_children == none: return node elif node.left_children.left_children == none: return node else: return self.best_left_right(node.left_children,type) else: if node.right_children == none: return node elif node.right_children.right_children == none: return node else: return self.best_left_right(node.right_children,type) # 前序(先中再左最后右) def front(self,node=none): if node == none: self.front_list = [] node = self.root # 输出当前节点 self.front_list.append(node.value) # 先判断左枝 if not node.left_children == none: self.front(node.left_children) # 再判断右枝 if not node.right_children == none: self.front(node.right_children) # 返回最终结果 return self.front_list # 中序(先左再中最后右) def middle(self,node=none): if node == none: node = self.root # 先判断左枝 if not node.left_children == none: self.middle(node.left_children) # 输出当前节点 self.middle_list.append(node.value) # 再判断右枝 if not node.right_children == none: self.middle(node.right_children) return self.middle_list # 后序(先左再右最后中) def after(self,node=none): if node == none: node = self.root # 先判断左枝 if not node.left_children == none: self.after(node.left_children) # 再判断右枝 if not node.right_children == none: self.after(node.right_children) self.after_list.append(node.value) return self.after_list # 节点删除 def del_node(self,v,node=none): if node == none: node = self.root # 删除根节点 if node.value == v: self.del_root(self.root) return # 删除当前节点的左节点 if node.left_children: if node.left_children.value == v: self.del_left(node) return # 删除当前节点的右节点 if node.right_children: if node.right_children.value == v: self.del_right(node) return if v > node.value: if node.right_children: self.del_node(v, node.right_children) else: print("删除的元素不存在") else: if node.left_children: self.del_node(v, node.left_children) else: print("删除的元素不存在") #删除当前节点的右节点 def del_right(self,node): # 情况1 删除节点没有右枝 if node.right_children.right_children == none: node.right_children = node.right_children.left_children else: best_left = self.best_left_right(node.right_children.right_children) # 表示右枝最左孙就是右枝本身 if best_left == node.right_children.right_children and best_left.left_children == none: node.right_children.value = best_left.value node.right_children.right_children = best_left.right_children else: node.right_children.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 删除当前节点的左节点 def del_left(self,node): # 情况1 删除节点没有右枝 if node.left_children.right_children == none: node.left_children = node.left_children.left_children else: best_left = self.best_left_right(node.left_children.right_children) # 表示右枝最左子孙就是右枝本身 if best_left == node.left_children.right_children and best_left.left_children == none: node.left_children.value = best_left.value node.left_children.right_children = best_left.right_children else: node.left_children.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 删除根节点 def del_root(self,node): if node.right_children == none: if node.left_children == none: node.value = none else: self.root = node.left_children else: best_left = self.best_left_right(node.right_children) # 表示右枝最左子孙就是右枝本身 if best_left == node.right_children and best_left.left_children == none: node.value = best_left.value node.right_children = best_left.right_children else: node.value = best_left.left_children.value best_left.left_children = best_left.left_children.right_children # 搜索 def search(self,v,node=none): if node == none: node = self.root if node.value == v: return true if v > node.value: if not node.right_children == none: return self.search(v, node.right_children) else: if not node.left_children == none: return self.search(v, node.left_children) return falseif __name__ == '__main__': # 需要建立二叉树的列表 list = [4, 6, 3, 1, 7, 9, 8, 5, 2] t = tree() t.create_tree(0,list) res = t.front() print('前序', res) |
执行结果:
前序 [4, 2, 1, 3, 7, 6, 5, 9, 8]
通过前序可以画出二叉树
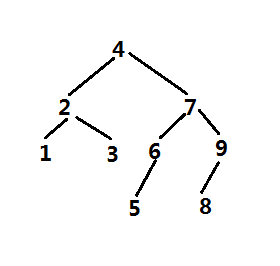
完美,哈哈。
这是我钻了两天才写出的代码,哈哈,努力还是有回报的,加油。
下一步就是代码优化了
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://www.cnblogs.com/7749ha/p/9179086.html













