本文为大家分享了Python遗传算法解决最大流问题,供大家参考,具体内容如下
Generate_matrix
|
1
2
3
4
|
def Generate_matrix(x,y): import numpy as np import random return np.ceil(np.array([random.random()*10 for i in range(x*y)]).reshape(x,y)) |
Max_road
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
def Max_road(A,degree,start): import random import numpy as np import copy def change(M,number,start): # number 控制变异程度 start 控制变异量 x , y = M.shape for i in range(start,x): Line = zip(range(len(M[i])),M[i]) index_0 = [t[0] for t in Line if t[1]==0] # 获取 0 所对应的下标 index_1 = [t[0] for t in Line if t[1]==1] # 获取 1 所对应的下标 M[i][random.sample(index_0,number)[0]]=1 # 随机改变序列中 number 个值 0->1 M[i][random.sample(index_1,number)[0]]=0 # 随机改变序列中 number 个值 1->0 return M x,y = A.shape n=x generation = y #初始化一个有 n 中情况的解决方案矩阵 init_solve = np.zeros([n,x+y-2]) init=[1]*(x-1)+[0]*(y-1) for i in range(n) : random.shuffle(init) init_solve[i,:] = init # 1 表示向下走 0 表示向右走 solve = copy.copy(init_solve) for loop in range(generation): Sum = [A[0,0]]*n # 用于记录每一种方案的总流量 for i in range(n): j=0;k=0; for m in solve[i,:]: if m==1: k=k+1 else: j=j+1 Sum[i] = Sum[i] + A[k,j] Sum_index = zip(range(len(Sum)),Sum) sort_sum_index = sorted(Sum_index,key = lambda d : d[1] , reverse =True) # 将 方案 按照流量总和排序 Max = sort_sum_index[0][1] # 最大流量 #print Max solve_index_half = [a[0] for a in sort_sum_index[:n/2]] # 保留排序后方案的一半 solve = np.concatenate([solve[solve_index_half],solve[solve_index_half]]) # 将保留的一半方案 进行复制 ,复制部分用于变异 change(solve,int((x+y-2)*degree)+1 ,start) # 变异 return solve[0] , Max |
Draw_road
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
def Draw_road(road,A): import pylab as plt import seaborn seaborn.set() x , y =A.shape # 将下移和右移映射到绘图坐标上 Road = [(1,x)] # 初始坐标 j=1;k=x; for m in road: if m==1: k=k-1 else: j=j+1 Road.append((j,k)) # print Road for i in range(len(road)): plt.plot([Road[i][0],Road[i+1][0]],[Road[i][1],Road[i+1][1]]) |
实际运行的例子
|
1
2
3
4
5
6
7
8
9
10
11
12
|
In [119]: A = Generate_matrix(4,6)In [120]: AOut[120]: array([[ 10., 1., 7., 10., 8., 8.], [ 4., 8., 8., 4., 8., 2.], [ 9., 8., 8., 3., 9., 8.], [ 7., 2., 5., 9., 3., 8.]])In [121]: road , M=Max_road(A,0.1,2)In [122]: Draw_road(road,A) |
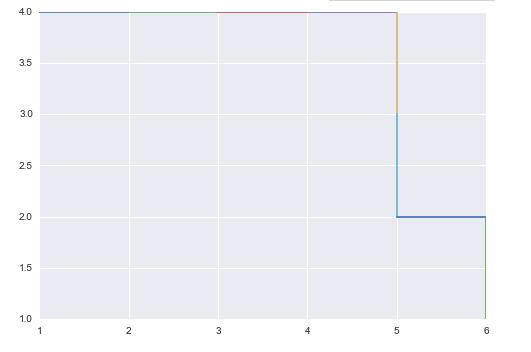
较大规模的情况
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
In [105]: A = Generate_matrix(40,60)In [106]: road , M=Max_road(A,0.1,4)In [107]: roadOut[107]: array([ 0., 0., 0., 1., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0., 0., 0., 1., 0., 0., 1., 0., 1., 1., 1., 1., 1., 0., 0., 0., 0., 0., 1., 0., 0., 1., 0., 0., 0., 1., 0., 0., 0., 1., 0., 1., 0., 0., 1., 0., 0., 1., 0., 0., 0., 1., 0., 0., 1., 1., 1., 1., 0., 0., 0., 0., 0., 0., 1., 0., 1., 1., 1., 1., 0., 1., 0., 1., 1., 1., 0., 1., 0., 1., 0., 1., 0., 1., 0., 0., 1., 0., 1., 0., 0., 1., 0., 1.])In [108]: Draw_road(road,A) |
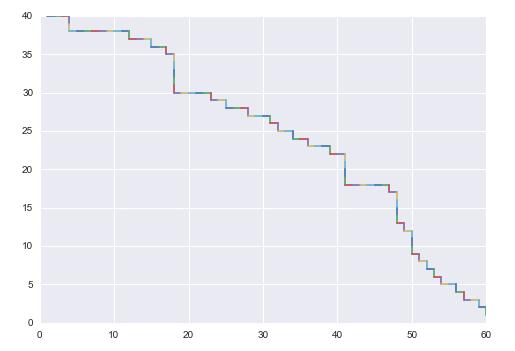
|
1
2
3
|
In [109]: A = generate_Matrix(100,200)In [110]: road , M=Max_road(A,0.1,10)In [111]: draw_road(road,A) |
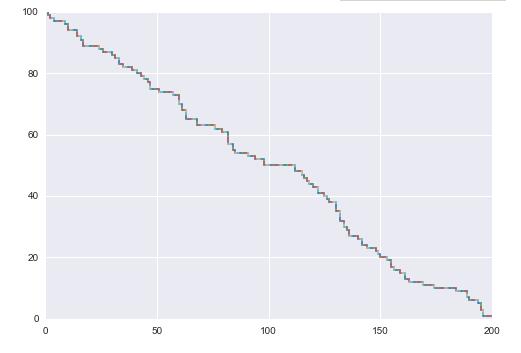
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://blog.csdn.net/u014135091/article/details/48733295










