傅立叶变换时数字信号处理的重要方法之一,是法国数学家傅立叶在1807年在法国科学学会上发表的一篇文章中所提出的,在文章中使用了正弦函数描述温度分布,而且提出了一个著名的论断:任何连续性的周期信号都可以由一组适当的正弦曲线组合而成。而这个论断被当时审查论文的著名数学家拉格朗日所否定,拉格朗日认为正弦函数无法组合成一个个带有棱角的信号,但是从无限逼近的角度考虑,可以使用正弦函数来非常逼近期直到表示方法不存在明显差异,这篇论文最终在在拉格朗日死后15年之久才得以发表。
傅立叶变换的分类
根据信号是是周期性以及连续还是离散的特点,将傅立叶变换进行延伸,变换分为如下四种

另外,根据使用的是实数还是复数,有分为实数傅立叶变换和复数傅立叶变换。
主要特点:fs
用于分析连续周期信号。时域上任意连续的周期信号可以分解为无限多个正弦信号之和,在频域上就表示为离散非周期的信号,即时域连续周期对应频域离散非周期的特点。
主要特点:ft
主要用于分析连续非周期信号,由于信号是非周期的,它必包含了各种频率的信号,所以具有时域连续非周期对应频域连续非周期的特点。
fs和ft 都是用于连续信号频谱的分析工具,都以傅立叶级数理论问基础推导出的。时域上连续的信号在频域上都有非周期的特点,但对于周期信号和非周期信号又有在频域离散和连续之分。
主要特点:dtft
它用于离散非周期序列分析,根据连续傅立叶变换要求连续信号在时间上必须可积这一充分必要条件,那么对于离散时间傅立叶变换,用于它之上的离散序列也必须满足在时间轴上级数求和收敛的条件;由于信号是非周期序列,它必包含了各种频率的信号,所以dtft对离散非周期信号变换后的频谱为连续的,即有时域离散非周期对应频域连续周期的特点。
主要特点:dft
假设了序列的周期无限性,但在处理时又对区间作出限定(主值区间),以符合有限长的特点,这就使dft带有了周期性。另 外,dft只是对一周期内的有限个离散频率的表示,所以它在频率上是离散的,就相当于dtft变换成连续频谱后再对其采样,此时采样频率等于序列延拓后的周期n,即主值序列的个数。
离散傅立叶变换dft
dft用于将信号从时域变换为频域,而且时域与频域都是离散的,可以确认出一个信号是由哪些正弦波叠加而成,而这些结果者反应为正弦波的振幅和相位等信息。而至于时域与频域,前者表示的是信号随时间动态变化的关系,在这种分析方式下,往往会随着时间的不同信号呈现不同的状态变化。而频域可以理解为正弦波的振幅,从傅立叶的论断中我们了解到,任何周期函数,都可能是由不同振幅和不同相位与角频率的正弦波的叠加,频域分析的一个主要结果是频谱,常见的频谱有两种:振幅相关的频谱与相位相关的频谱。比如正弦曲线可表示为y=asin(ωx+φ)+k,具体的实际意义如下所示:
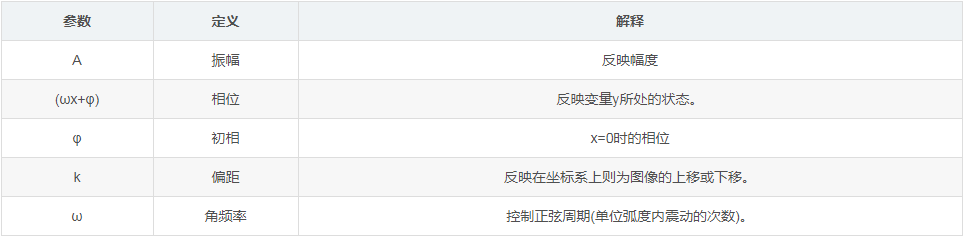
理解辅助:变形的谐波函数
谐波(harmonic wave)是指电流中所含有的频率为基波的整数倍的电量,一般是指对周期性的非正弦电量进行傅里叶级数分解,其余大于基波频率的电流产生的电量。如下可以看出动态的三角函数的图形变换,可以加深对傅立叶论断的理解。
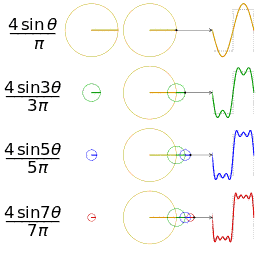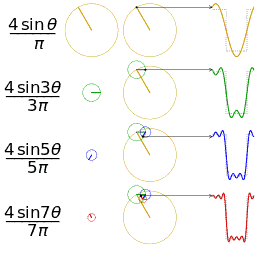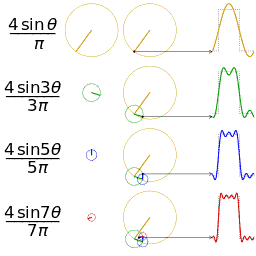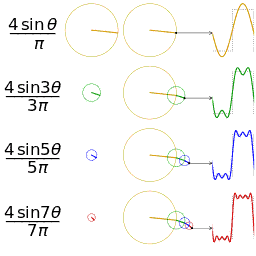
理解辅助:振幅的频谱
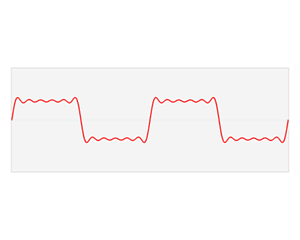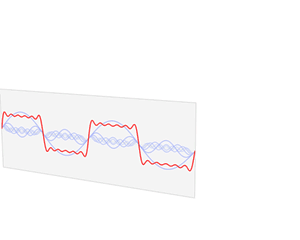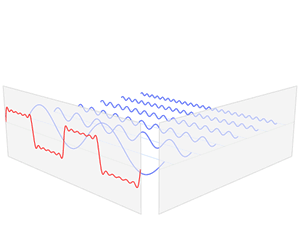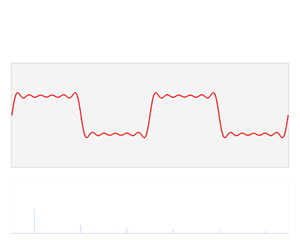
而至于如何求取频谱,由于三角函数具有正交性,相互之间不具影响,根据此特性结合下图,对于振幅的频谱则可有直观的了解。而至于初相相关的频谱,可以以此为基础,不难理解。
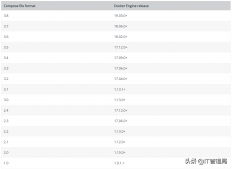
快速傅立叶变换fft
fft(fast fourier transform)实际只是dft的改善。是1965年由库利和图基共同提出的一种快速计算dft的方法。这种方法充分利用了dft运算中的对称性和周期性,从而将dft运算量从n2减少到n*log2n。当n比较小时,fft优势并不明显。但当n大于32开始,点数越大,fft对运算量的改善越明显。比如当n为1024时,fft的运算效率比dft提高了100倍。
应用领域和局限
傅立叶变化在很多领域都有很好的应用,比如图像优化和音频降噪等等,但是由于傅立叶变换的模型建立在平稳信号基础上的,对于非平稳信号的分析具有很大的局现性。
总结
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,谢谢大家对服务器之家的支持。如果你想了解更多相关内容请查看下面相关链接
原文链接:https://blog.csdn.net/liumiaocn/article/details/80440879