图 1 显示的是正态(或高斯)分布。它是一条连续的贝尔曲线,期望两边的值是相等的,可以理解为期望就是平均值。它是一个概率分布,因此曲线下方的面积是1。正态分布是由两个参数完全定义的:期望和标准差,它们是衡量期望两边的值如何分布的一种方式。
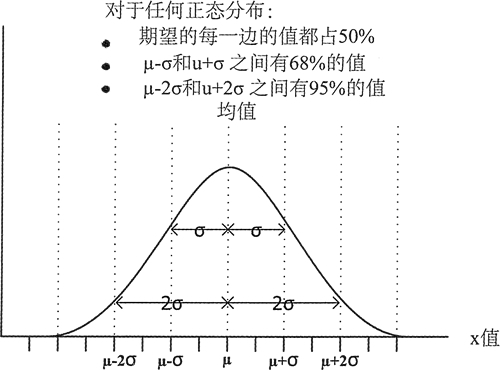
图 1 正态分布
期望和标准差分别是用希腊字母 μ 和 σ 来表示的,变量 x 有 n 个样本,这些是由下面的公式定义的:
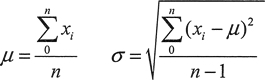
因此,期望就是值的和除以值的个数一换句话说,也就是平均值。可以通过值和期望的差值的平方子和除以 n-1,然后对结果开方来得到标准差。对于不同的期望和标准差的值,正态分布的相对宽度和高度分布曲线的变化是相当大的。但是,分布值总是如图 1 所示。这意味着,如果知道一个符合正态分布的变量的期望和标准差,例如在大量人口中个体的身高,就可以知道 95% 的人身高不超过期望的 2σ。标准正态分布的期望为 0,标准差为 1。
uniform_distribution 模板定义了可以产生随机浮点值的分布对象类型,默认是 double 类型。默认构造函数创建的是标准正态分布,因此期望是 0,方差是 1.0:
|
1
|
std::normal_distribution<> dist; // mu: 0 sigma: 1 |
下面展示了如何创建一个有特定值和标准差的正态分布:
|
1
2
|
double mu {50.0}, sigma {10.0};std::normal_distribution<> norm {mu, sigma}; |
这里定义了一个生成 double 值的分布对象,期望为 50.0,标准差是 10.0。为了生成值,可以将一个随机数生成器传给 norm 函数对象。例如:
|
1
2
3
|
std::random_device rd;std::default_random_engine rng {rd()};std::cout << "Normally distributed values: "<< norm (rng) << " " << norm (rng) << std::endl; // 39.6153 45.5608 |
可以通过调用对象的成员函数 mean() 和 stddev() 来获取它的期望值和标准差:
|
1
|
std::cout<<"mu: "<< norm.mean () << " sigma: " << norm.stddev ()<< std::endl; // mu: 50 sigma: 10 |
通过调用无参数的成员函数 param(),可以得到一个封装了这两个值的 param_type 对象。为了设置期望或标准差,需要将一个 param_type 对象传给成员函数 Pamm()。分布类有用来获取期望和标准差的成员,param_type 对象拥有和它们的名字相同的成员函数。下 面是一个示例:
|
1
2
3
4
5
6
|
using Params = std::normal_distribution<>::param_type; // Type alias for readabilitydouble mu {50.0}, sigma {10.0};std::normal_distribution<> norm {mu, sigma};// Create distributionauto params = norm.param(); // Get mean and standard deviationnorm.param(Params {params.mean(),params.stddev() + 5.0}); // Modify paramsstd::cout << "mu: "<< norm.mean() << " sigma: " << norm.stddev ()<< std::endl; // mu: 50 sigma: 15 |
这里调用无参数的 param() 来获取包含期望和方差的 param_type 对象。在第二个 param() 调用中,通过传入一个 Pams 对象将标准差增加了 5.0。
可以通过传入一个 param_type 对象作为一个分布对象调用的第二个参数来临时设置期望和标准差:
|
1
2
3
4
5
6
7
|
using Params = std::normal_distribution<>::param_type; // Type alias for readabilitystd::random_device rd;std::default_random_engine rng {rd()};std::normal_distribution<> norm {50.0, 10.0}; // Create distributionParams new_p {100.0, 30.0};// mu=100 sigma=30std::cout << norm(rng, new_p) << std::endl; // Generate value with new_p: 100.925std::cout << norm,mean() << " " << norm.stddev()<< std::endl;// 50 10 |
new_p 定义的期望和标准差只会被应用到它被作为第二个参数传入的 norm 的执行中。原始的期望和标准差会被应用到随后的没有第二个参数的 norm 调用中。
成员函数 min() 和 max() 返回的是分布可以产生的最小值和最大值。对于分布来说,这并不是特别有用。因为返回值的类型可以这样表示最大值和最小值:
|
1
|
std::cout << "min: " << norm.min () << " max: " << norm.max ()<< std::endl; // min:4.94066e-324 max: 1.7 9769e+308 |
总结
到此这篇关于C++ normal_distribution高斯正态分布函数的文章就介绍到这了,更多相关C++ normal_distribution高斯正态分布函数内容请搜索服务器之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持服务器之家!
原文链接:http://c.biancheng.net/view/643.html














