Floyd算法直接使用二维数组求出所有顶点到所有顶点的最短路径。
D代表顶点到顶点的最短路径权值和的矩阵。
P代表对应顶点的最小路径的前驱矩阵。
以下程序在DEV C++中调试运行通过。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
|
#include <stdio.h> #define INFINITY 65535 typedef int VertexType; //顶点是字符型 typedef int EdgeType; //边是整型 typedef struct //图的邻接矩阵存储结构 { VertexType vexs[9]; //顶点向量 EdgeType edges[9][9]; //邻接矩阵 int vexnum,arcnum; //图中当前的顶点数和边数 }MGraph; /* 邻接矩阵的建立*/ void CreateGraph(MGraph *G) { int i,j,k,weight; int ch1,ch2; printf("请输入顶点数和边数(输入格式为:顶点数,边数):"); scanf("%d,%d",&(G->vexnum),&(G->arcnum)); printf("请输入顶点名称(输入格式为:a,b,c...):"); for(i=0;i<G->vexnum;i++) { getchar(); scanf("%d",&(G->vexs[i])); } for(i=0;i<G->vexnum;i++) for(j=0;j<G->vexnum;j++) if(i==j) G->edges[i][j]=0; else G->edges[i][j]=INFINITY; printf("请输入每条边对应的两个顶点名称(输入格式为:a,b):\n"); for(k=0;k<G->arcnum;k++) { // getchar(); printf("请输入第%d条边的两个顶点名称:",k+1); scanf("%d,%d",&ch1,&ch2); for(i=0;ch1!=G->vexs[i];i++); for(j=0;ch2!=G->vexs[j];j++); getchar(); printf("请输入第%d条边的权值:",k+1); scanf("%d",&weight); G->edges[i][j]=weight; G->edges[j][i]=weight; } } void ShortestPath_Floyd(MGraph G,int P[9][9],int D[9][9]) { int v,w,k; for(v=0;v<G.vexnum;v++)//初始化D和P { for(w=0;w<G.vexnum;w++) { D[v][w]=G.edges[v][w]; P[v][w]=w; } } for(k=0;k<G.vexnum;k++) { for(v=0;v<G.vexnum;v++) { for(w=0;w<G.vexnum;w++) { if(D[v][w]>(D[v][k]+D[k][w])) {//如果经过下标为k顶点路径比原两点间路径更短,将当前两点间权值设为更小的一个 D[v][w]=D[v][k]+D[k][w]; P[v][w]=P[v][k]; } } } } } void main() { MGraph G; CreateGraph(&G); int i,j; printf("edgesnum:%d\n",G.arcnum); printf("vexesnum:%d\n",G.vexnum); for(i=0;i<9;i++) { for(j=0;j<9;j++) printf("%d ",G.edges[i][j]); printf("\n"); } int v,w,k; int P[9][9]; int D[9][9]; printf("%d\n",P); printf("%d\n",D); ShortestPath_Floyd(G,P,D); for(v=0;v<G.vexnum;v++)//显示路径 { for(w=v+1;w<G.vexnum;w++) { printf("v%d-v%d weight:%d ",v,w,D[v][w]); k=P[v][w]; printf("path:%d",v); while(k!=w) { printf("->%d",k); k=P[k][w]; } printf("->%d\n",w); } } } |
运行结果如图所示。
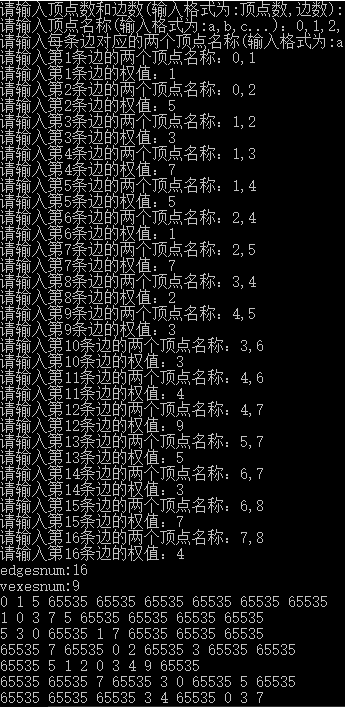
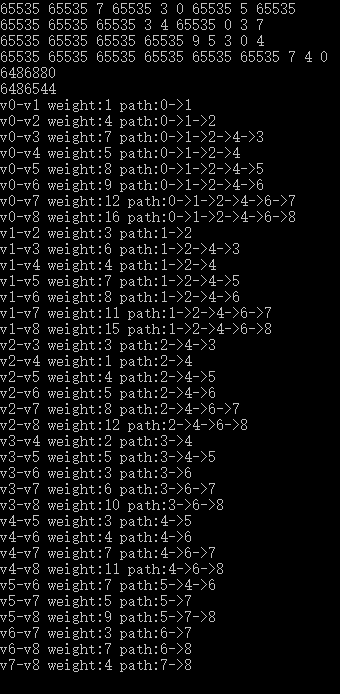
整个算法的时间复杂度是O(n^3)。
在编写过程中遇到了以下错误:
在62行
[Error]subscripted value is neither array nor pointer nor vector
意思是
下标的值不是数组或指针或向量
当时我这一行是这样写的
void ShortestPath_Floyd(MGraph G,int** P,int** D)
因为在上一篇文章Dijkstra算法中一维数组作为函数参数是用的int*,没有问题
所以在这里二维数组我就想当然地用了int**
但是如果参数传入int**类型,在函数里就不能使用P[v][w]访问二维数组的值
编译器不能正确为它寻址,需要模仿编译器的行为把P[v][w]这样的式子手工转变为:
*((int*)P + n*v + w);
所以在被调用函数中对形参数组定义时可以指定所有维数的大小,也可以省略第一维的大小说明
故改为void ShortestPath_Floyd(MGraph G,int P[9][9],int D[9][9])就可以编译通过。
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持服务器之家。
原文链接:http://blog.csdn.net/HEYIAMCOMING/article/details/76584531














