二叉查找树性质
1、二叉树
每个树的节点最多有两个子节点的树叫做二叉树。
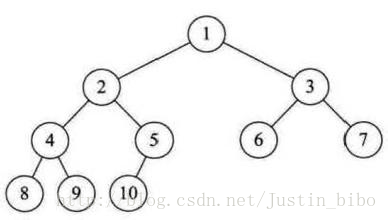
2、二叉查找树
一颗二叉查找树是按照二叉树的结构来组织的,并且满足一下性质:
一个节点所有左子树上的节点不大于盖节点,所有右子树的节点不小于该节点。
对查找树的操作查询,插入,删除等操作的时间复杂度和树的高度成正比, 因此,构建高效的查找树尤为重要。
查找树的遍历
先序遍历
查找树的遍历可以很简单的采用递归的方法来实现。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};void preorder(struct list *t)//t为根节点的指针{ if(t!=NULL) { printf("%d,",t->a); preorder(t->left); perorder(t->right); }} |
中序遍历
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};void preorder(struct list *t)//t为根节点的指针{ if(t!=NULL) { preorder(t->left); printf("%d,",t->a); perorder(t->right); }} |
后序遍历
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};void preorder(struct list *t)//t为根节点的指针{ if(t!=NULL) { preorder(t->left); perorder(t->right); printf("%d,",t->a); }} |
查找树的搜索
给定关键字k,进行搜索,返回结点的指针。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};struct list * search(struct list *t,int k){ if(t==NULL||t->a==k) return t; if(t->a<k) search(t->right); else search(t>left);}; |
也可以用非递归的形式进行查找
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};struct list * search(struct list *t,int k){ while(true) { if(t==NULL||t->a==k) { return t; break; } if(t->a<k) t=t->rigth; else t=t->left; }}; |
最大值和最小值查询
根据查找树的性质,最小值在最左边的结点,最大值的最右边的 结点,因此,可以直接找到。
下面是最大值的例子:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};struct lsit *max_tree(struct lsit *t){ while(t!=NULL) { t=t->right; } return t;}; |
查找树的插入和删除
插入和删除不能破坏查找树的性质,因此只需要根据性质,在树中找到相应的位置就可以进行插入和删除操作。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
struct list{ struct list *left;//左子树 struct list *right;//右子树 int a;//结点的值};void insert(struct list *root,struct list * k){ struct list *y,*x; x=root; while(x!=NULL) { y=x; if(k->a<x->a) { x=x->left; } else x=x->right; } if(y==NULL) root=k; else if(k->a<y->a) y->left=k; else y->right=k;} |
感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!














