二叉树的一些概念
二叉树就是每个结点最多有两个子树的树形存储结构。先上图,方便后面分析。
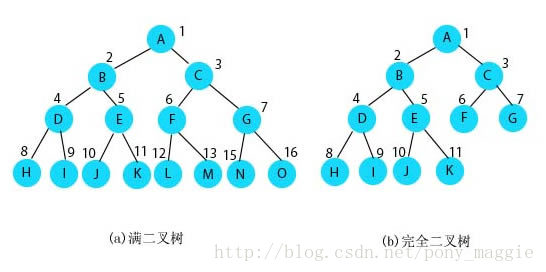
1 满二叉树和完全二叉树
上图就是典型的二叉树,其中左边的图还叫做满二叉树,右边是完全二叉树。然后我们可以得出结论,满二叉树一定是完全二叉树,但是反过来就不一定。满二叉树的定义是除了叶子结点,其它结点左右孩子都有,深度为k的满二叉树,结点数就是2的k次方减1。完全二叉树是每个结点都与深度为k的满二叉树中编号从1到n一一对应。
2 树的深度
树的最大层次就是深度,比如上图,深度是4。很容易得出,深度为k的树,拥有的最大结点数是2的k次方减1。
3 树的孩子,兄弟,双亲
上图中,B,C是A的孩子,B,C之间互为兄弟,A是B,C的双亲。
二如何创建二叉树
先说说二叉树的存储结构,跟很多其它模型一样,也有顺序和链式两种方式。前者虽然使用简单,但是存在浪费空间的问题,举个例子,下图的二叉树,用顺序的方式存储(0表示空,没有子树)是:
1 2 3 4 5 6 7 0 0 0 0 8 0 0 0
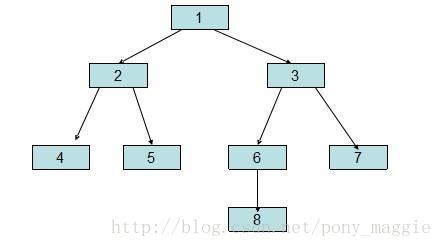
是不是相当浪费空间呢。
链式结构可以定义如下:
|
1
2
3
4
5
6
|
typedef struct _BiTNode { int data; _BiTNode *leftChild; _BiTNode *rightChild; }BiTNode, *pBiTree; |
然后就可以写一个函数来创建二叉树,过程是在控制台输入a表示退出当前这一层,不再为该层创建左右孩子。输入其它字母表示继续创建。比如下面的输入序列:
创建了如下结构的二叉树,
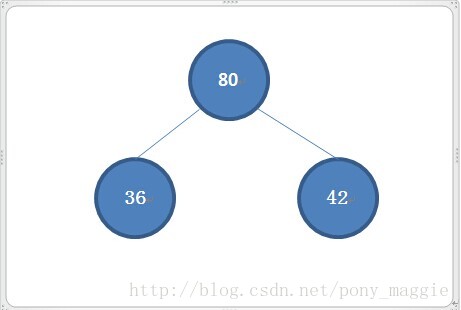
每个结点里的数值是随机生成的小于100的数字。同时我也写了一个自动的命令序列函数,方便测试,不用手动输入,非自动和自动创建的函数如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
//创建二叉树, 先序顺序 int CreateBiTree(pBiTree *root) { char ch = 0; fflush(stdin); if ((ch = getchar()) == 'a')//控制树的结构 { *root = NULL; } else { *root = (BiTNode *)malloc(sizeof(BiTNode)); if (!(*root)) { return RET_ERROR; } (*root)->data = GetRandom(); CreateBiTree(&(*root)->leftChild); CreateBiTree(&(*root)->rightChild); } return RET_OK; } int g_i = 0; //创建二叉树,自动执行,方便测试 int CreateBiTreeAuto(pBiTree *root) { char szOrder[] = "bbaabaa"; char ch = 0; if (szOrder[g_i++] == 'a')//控制树的结构 { *root = NULL; } else { *root = (BiTNode *)malloc(sizeof(BiTNode)); if (!(*root)) { return RET_ERROR; } (*root)->data = GetRandom(); CreateBiTreeAuto(&(*root)->leftChild); CreateBiTreeAuto(&(*root)->rightChild); } return RET_OK; } |
三遍历顺序
先序遍历
先序遍历是先访问根结点,再左子树,再右子树,比如图1中的右图,先序遍历的输出如下:
A,B,D,H,I,E,J,K,C,F,G
根据上面的思想,很容易用递归的形式写出先序遍历的代码:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
//先序遍历 int PreOrderVisitTree(pBiTree T, VisitType pFuncVisit) { if (T) { (*pFuncVisit)(T->data); if (PreOrderVisitTree(T->leftChild, pFuncVisit) == RET_OK) { if (PreOrderVisitTree(T->rightChild, pFuncVisit) == RET_OK) { return RET_OK; } } return RET_ERROR; } else { return RET_OK; } } |
中序遍历和后序遍历
有了先序的经验,这两个就很好理解了,中序是先访问左子树, 再根结点,再右子树, 后序是先访问左子树, 再右子树,再根结点。代码更容易,只要改一下调用顺序就可以了。
不过我这里给出一种非递归的实现。递归固然是清晰明了,但是存在效率低的问题,非递归的方案用栈结构来存结点信息,通过出栈访问来遍历二叉树。它思想是这样的,当栈顶中的指针非空时,遍历左子树,也就是左子树根的指针进栈。当栈顶指针为空时,应退至上一层,如果是从左子树返回的,访问当前层,也就是栈顶中的根指针结点。如果是从右子树返回,说明当前层遍历完毕,继续退栈。代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
//中序遍历, 非递归实现 int InOrderVisitTree(pBiTree T, VisitType pFuncVisit) { ponyStack binaryTreeStack; InitStack(&binaryTreeStack, 4); Push(&binaryTreeStack, &T); pBiTree pTempNode; while (!IsEmptyStack(binaryTreeStack)) { while((GetTop(binaryTreeStack, &pTempNode) == RET_OK) && (pTempNode != NULL)) { Push(&binaryTreeStack, &(pTempNode->leftChild)); } Pop(&binaryTreeStack, &pTempNode); if (!IsEmptyStack(binaryTreeStack)) { Pop(&binaryTreeStack, &pTempNode); (*pFuncVisit)(pTempNode->data); Push(&binaryTreeStack, &(pTempNode->rightChild)); } } return RET_OK; } |
感谢阅读,希望能帮助到大家,谢谢大家对本站的支持!














