基于拉链式和线性探测式散列表实现Map_Java教程

基于拉链式和线性探测式散列表实现Map

前言

前几篇我们一起学习了基于数组、链表、二叉树、红黑树来实现Map的操作，本篇我们将会一起来学习基于散列表来实现Map，这种方式对应着java里面的HashMap，这也是使用最多的一种方式

散列表实现Map主要分为了两个步骤:

基于散列函数将被查找键转换为数组的下标
处理散列值冲突的情况，有两种方式来处理冲突：拉链式和线性探测

散列函数

实现散列表的第一步就是需要考虑如何把一个键转换为数组的下标，这时候就需要使用到散列函数，先把键值转换成一个整数然后在使用除留余数法计算出数组的下标。每种类型的键我们都需要一个不同的散列函数。

在java中对于常用的数据类型已经实现了hashCode，我们只需要根据hashCode的值使用除留余数法即可转换成数组的下标

java中的约定：如果两个对象的equals相等，那么hashCode一定相同;如果hashCode相同，equals不一定相同。对于自定义类型的键我们通常需要自定义实现hashCode和equals;默认的hashCode返回的是对象的内存地址，这种散列值不会太好。

下面我来看看Java中常用类型的hashCode计算方式

Integer

由于hashCode需要返回的值就是一个int值，所以Integer的hashCode实现很简单，直接返回当前的value值

@Override
public int hashCode() {
return Integer.hashCode(value);
}
public static int hashCode(int value) {
return value;
}

Long

Java中Long类型的hashCode计算是先把值无符号右移32位，之后再与值相异或，保证每一位都用用到，最后强制转换成int值

@Override
public int hashCode() {
return Long.hashCode(value);
}
public static int hashCode(long value) {
return (int)(value ^ (value >>> 32));
}

Double、Float

浮点类型的键java中hashCode的实现是将键表示为二进制

public static int hashCode(float value) {
return floatToIntBits(value);
}
public static int floatToIntBits(float value) {
int result = floatToRawIntBits(value);
// Check for NaN based on values of bit fields, maximum
// exponent and nonzero significand.
if ( ((result & FloatConsts.EXP_BIT_MASK) ==
FloatConsts.EXP_BIT_MASK) &&
(result & FloatConsts.SIGNIF_BIT_MASK) != 0)
result = 0x7fc00000;
return result;
}

String

java中每个char都可以表示成一个int值，所以字符串转换成一个int值

public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
char val[] = value;
for (int i = 0; i < value.length; i++) {
h = 31 * h + val[i];
}
hash = h;
}
return h;
}

软缓存

如果计算一个散列值比较耗时，那么我可以这个计算好的值缓存起来，即使用一个变量把这个值保存起来，在下一次调用时直接返回。Java中的String就是采用的这种方式。

拉链式的散列表

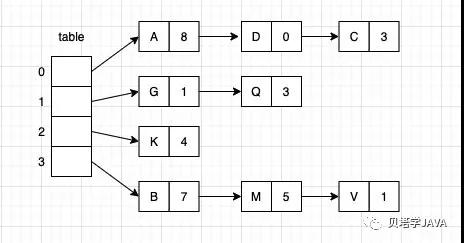
散列函数能够将键值转换成数组的下标;第二步就是需要处理碰撞冲突，也就是需要处理遇到了两个散列值相同的对象应该如何存储。有一种方式是数组中的每一个元素都指向一个链表用来存放散列值相同的对象，这种方式被称为拉链法

拉链法可以使用原始的链表保存键，也可以采用我们之前实现的红黑树来表示，在java8中采用的这两种方式的混合，在节点数超过了8之后变为红黑树。

这里我们就采用简单的链表来实现拉链式散列表，数据结构使用在前几篇中已经实现的LinkedMap，可以参考前面的文章《基于数组或链表实现Map》。

基于拉链式和线性探测式散列表实现Map

public class SeparateChainingHashMap<K, V> implements Map<K, V> {
private int size;
private LinkedMap<K, V>[] table;
public SeparateChainingHashMap(int capacity) {
this.table = (LinkedMap<K, V>[]) new LinkedMap[capacity];
for (int i = 0; i < capacity; i++) {
this.table[i] = new LinkedMap<>();
}
}
@Override
public void put(K key, V value) {
this.table[hash(key)].put(key, value);
size++;
}
private int hash(K key) {
return (key.hashCode() & 0x7fffffff) % table.length;
}
@Override
public V get(K key) {
return this.table[hash(key)].get(key);
}
@Override
public void delete(K key) {
this.table[hash(key)].delete(key);
size--;
}
@Override
public int size() {
return size;
}
}

这的hash函数使用key的hashCode与上0x7fffffff得到一个非负的整数，然后再使用除留余数法计算出数组的下标。其中0x7FFFFFFF 的二进制表示就是除了首位是 0，其余都是1，也就是说，这是最大的整型数 int(因为第一位是符号位，0 表示他是正数),可以使用Integer.MAX_VALUE代替

散列表的主要目的在于把键值均匀的分布到数组中，所以散列表是无序的，如果你需要的Map需要支持取出最大值，最小值，那么散列表都不适合。

这里我们实现的拉链式散列表的数组大小是固定的，但是通常在随着数据量的增大，越短的数组出现碰撞的几率会增大，所以需要数组支持动态的扩容，扩容之后需要把原来的值重新插入到扩容之后的数组中。数组的扩容可以参考之前的文章《老哥是时候来复习下数据结构与算法了》

线性探测式散列表

实现散列表的另一种方式就是用大小为M来保存N个键值，其中M>N;解决碰撞冲突就需要利用数组中的空位;这种方式中最简单的实现就是线性探测。

线性探测的主要思路：当插入一个键，发生碰撞冲突之后直接把索引加一来检查下一个位置，这时候会出现三种情况:

下一个位置和待插入的键相等，那么值就修改值

下一个位置和待插入的键不相等，那么索引加一继续查找

如果下一个位置还是一个空位，那么直接把待插入对象放入到这个空位

初始化

线性探测式散列表使用两个数组来存放keys和values，capacity表示初始化数组的大小

private int size;
private int capacity;
private K[] keys;
private V[] values;
public LinearProbingHashMap(int capacity) {
this.capacity = capacity;
this.keys = (K[]) new Object[capacity];
this.values = (V[]) new Object[capacity];
}

插入

当插入键的位置超过了数组的大小，就需要回到数组的开始位置继续查找，直到找到一个位置为null的才结束;index = (index + 1) % capacity

当数组已存放的容量超过了数组总容量的一半，就需要扩容到原来的2倍

@Override
public void put(K key, V value) {
if (Objects.isNull(key)) {
throw new IllegalArgumentException("Key can not null");
}
if (this.size > this.capacity / 2) {
resize(2 * this.capacity);
}
int index;
for (index = hash(key); this.keys[index] != null; index = (index + 1) % capacity) {
if (this.keys[index].equals(key)) {
this.values[index] = value;
return;
}
}
this.keys[index] = key;
this.values[index] = value;
size++;
}

动态调整数组的大小

我们可以参考之前在文章《老哥是时候来复习下数据结构与算法了》中实现的动态调整数据的大小;在线性探测中需要把原来的数据重新插入到扩容之后的数据，因为数组的大小变了需要重新计算索引的位置。

private void resize(int cap) {
LinearProbingHashMap<K, V> linearProbingHashMap = new LinearProbingHashMap<>(cap);
for (int i = 0; i < capacity; i++) {
linearProbingHashMap.put(keys[i], values[i]);
}
this.keys = linearProbingHashMap.keys;
this.values = linearProbingHashMap.values;
this.capacity = linearProbingHashMap.capacity;
}

查询

线性探测散列表中实现查询的思路：根据待查询key的hash函数计算出索引的位置，然后开始判断当前位置上的key是否和待查询key相等，如果相等那么就直接返回value，如果不相等那么就继续查找下一个索引直到遇到某个位置是null才结束，表示查询的key不存在;

@Override
public V get(K key) {
if (Objects.isNull(key)) {
throw new IllegalArgumentException("Key can not null");
}
int index;
for (index = hash(key); this.keys[index] != null; index = (index + 1) % capacity) {
if (this.keys[index].equals(key)) {
return this.values[index];
}
}
return null;
}

删除元素

线性探测式的删除稍微麻烦一些，首先需要查找出待删除的元素位置，删除元素之后需要把当前索引之后的连续位置上的元素重新插入;因为是否有空位对于线性探测式散列表的查找至关重要;例如：5->7->9，删除了7之后，如果不重新插入7的位置就是空位，那么get方法将无法查询到9这个元素;

每次删除之后都需要检测一次数组中实际元素的个数，如果与数组的容量相差较大，就可以进行缩容操作;

@Override
public void delete(K key) {
if (Objects.isNull(key)) {
throw new IllegalArgumentException("Key can not null");
}
int index;
for (index = hash(key); this.keys[index] != null; index = (index + 1) % capacity) {
if (this.keys[index].equals(key)) {
this.keys[index] = null;
this.values[index] = null;
break;
}
}
for (index = (index + 1) % capacity; this.keys[index] != null; index = (index + 1) % capacity) {
this.size--;
this.put(this.keys[index], this.values[index]);
this.keys[index] = null;
this.values[index] = null;
}
this.size--;
if (size > 0 && size < capacity / 4) {
resize(capacity / 2);
}
}